如圖1，灌溉車沿著平行于綠化帶底部邊線l的方向行駛，為綠化帶澆水．噴水口H離地豎直高度為h（單位：m）．如圖2，可以把灌溉車噴出水的上、下邊緣抽象為平面直角坐標系中兩條拋物線的部分圖象；把綠化帶橫截面抽象為矩形DEFG，其水平寬度DE=3m,豎直高度為EF的長．下邊緣拋物線是由上邊緣拋物線向左平移得到，上邊緣拋物線最高點A離噴水口的水平距離為2m,高出噴水口0.5m,灌溉車到l的距離OD為d（單位：m）．
（1）若h=1.5，EF=0.5m.
①求上邊緣拋物線的函數解析式，并求噴出水的最大射程OC；
②求下邊緣拋物線與x軸的正半軸交點B的坐標；
（2）若EF=1m.要使灌溉車行駛時噴出的水能澆灌到整個綠化帶，請直接寫出h的最小值．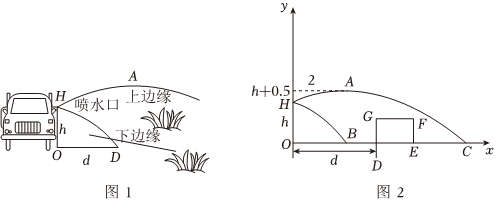
【考點】二次函數的應用．
【答案】（1）①上邊緣拋物線的函數解析式為y=-（x-2）2+2，噴出水的最大射程OC為6m；②點B的坐標為（2，0）；（3）．
1
8
65
32
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/3 19:0:1組卷：90引用：1難度：0.5
相似題
-
1．【問題背景】為了保持室內空氣的清新，某倉庫的門動換氣窗采用了以下設計：
如圖1，窗子的形狀是一個五邊形，它可看作是由一個矩形ABCD和一個△CDE組成，該窗子關閉時可以完全密封，根據室內的溫度和濕度也可以自動打開窗子上的通風口換氣．通風口為△FMN（陰影部分均不通風），點F為AB的中點，MN是可以沿窗戶邊框上下滑動且始終保持和AB平行的伸縮橫桿．
設窗子的邊框AB、AD分別為a m,b m,窗子的高度（窗子的最高點到邊框AB的距離）為c m.
【初步探究】
（1）若a=3，b=2，c=4（即點E到AB的距離為4）．
①MN與AB之間的距離為1m,求此時△FMN的面積；
②MN與AB之間的距離為x m,試將通風口的面積y m2表示成關于x的函數；
③伸縮桿MN移動到什么位置時，通風口面積最大，最大面積是多少？
【拓展提升】
（2）若金屬桿MN移動到高于CD所在位置的某一處時通風口面積達到最大值．
①c需要滿足的條件是 ，通風口的最大面積是 m2（用含a、b、c的代數式表示）
②用直尺和圓規在圖3中作出通風口面積最大金屬桿MN所在的位置，（保留作圖痕跡，不寫作法）發布：2025/5/24 17:0:2組卷：518引用：3難度：0.3 -
2．甲經銷商庫存有1200套A品牌服裝，每套進價400元，每套售價500元，一年內可賣完．現市場上流行B品牌服裝，每套進價300元，每套售價600元，但一年內只允許經銷商一次性訂購B品牌服裝，一年內B品牌服裝銷售無積壓．因甲經銷商無流動資金，只有低價轉讓A品牌服裝，用轉讓來的資金購進B品牌服裝，并銷售．經與乙經銷商協商，甲、乙雙方達成轉讓協議，轉讓價格y（元/套）與轉讓數量x（套）之間的函數關系式為y=
．若甲經銷商轉讓x套A品牌服裝，一年內所獲總利潤為w（元）．-110x+360（100≤x≤1200）
（1）求轉讓后剩余的A品牌服裝的銷售款Q1（元）與x（套）之間的函數關系式；
（2）求B品牌服裝的銷售款Q2（元）與x（套）之間的函數關系式；
（3）求w（元）與x（套）之間的函數關系式，并求w的最大值．發布：2025/5/24 17:0:2組卷：657引用：8難度：0.3 -
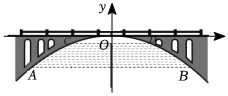3．如圖，有一座拋物線型拱橋，在正常水位時水面寬AB=20m,當水位上升3m時，水面寬CD=10m.
（1）按如圖所示的直角坐標系，求此拋物線的函數表達式；
（2）有一條船以5km/h的速度向此橋徑直駛來，當船距離此橋35km時，橋下水位正好在AB處，之后水位每小時上漲0.25m,當水位達到CD處時，將禁止船只通行．如果該船的速度不變繼續向此橋行駛35km時，水面寬是多少？它能否安全通過此橋？發布：2025/5/24 16:30:1組卷：2601引用：3難度：0.5