試卷征集
          
                
          
            
          
            
          
                
          
                    
                    
          加入會員
          
                
          
            
          
            
          
                
          
                    
                    
          操作視頻
          
                
          
            
          
        
          
    
          

    
          
        
    
          
    
          
    
          
        
          
            



          
    
          
        
          
            
          共享單車是指企業在校園、地鐵站點、公交站點、居民區、商業區、公共服務區等提供自行車單車共享服務，是共享經濟的一種新形態．一個共享單車企業在某個城市就“一天中一輛單車的平均成本（單位：元）與租用單車的數量（單位：千輛）之間的關系”進行調查研究，在調查過程中進行了統計，得出相關數據見下表：
          
  
    
          
      租用單車數量x（千輛）
      2
      3
      4
      5
      8
    
          
    
          
      每天一輛車平均成本y（元）
      3.2
      2.4
      2
      1.9
      1.7
    
          
            

          根據以上數據，研究人員分別借助甲、乙兩種不同的回歸模型，得到兩個回歸方程，方程甲：
          ?
          y
          （1）=
          4
          x
          +1.1，方程乙：
          ?
          y
          （2）=
          6
          .
          4
          x
          2
          +1.6．
          （1）為了評價兩種模型的擬合效果，完成以下任務：
          ①完成下表（計算結果精確到0.1）（備注：
          ?
          e
          i
          =yi-
          ?
          y
          i
          ，
          ?
          e
          i
          稱為相應于點（xi，yi）的殘差（也叫隨機誤差）； 
          
  
    
          
      租用單車數量x（千輛）
      2
      3
      4
      5
      8
    
          
    
          
      每天一輛車平均成本y（元）
      3.2
      2.4
      2
      1.9
      1.7
    
          
    
          
      模型甲
      估計值
          ?
          y
          i
          （1）          		
      
      2.4
      2.1
      
      1.6
    
          
    
          
      殘差
          ?
          e
          i
          （1）          		
      
      0
      -0.1
      
      0.1
    
          
    
          
      模型乙
      估計值
          ?
          y
          i
          （2）          		
      
      2.3
      2
      1.9
      
    
          
    
          
      殘差
          ?
          e
          i
          （2）          		
      
      0.1
      0
      0
      
    
          
            

          ②分別計算模型甲與模型乙的殘差平方和Q1及Q2，并通過比較Q1，Q2的大小，判斷哪個模型擬合效果更好．
          （2）這個公司在該城市投放共享單車后，受到廣大市民的熱烈歡迎，共享單車常常供不應求，于是該公司研究是否增加投放．根據市場調查，這個城市投放8千輛時，該公司平均一輛單車一天能收入8.4元；投放1萬輛時，該公司平均一輛單車一天能收入7.6元．問該公司應該投放8千輛還是1萬輛能獲得更多利潤？（按（1）中擬合效果較好的模型計算一天中一輛單車的平均成本，利潤=收入-成本）．
          【答案】見試題解答內容
          【解答】
          【點評】
          聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
          發布：2024/4/20 14:35:0組卷：264引用：3難度：0.1
          
        
          
            
          
                
          相似題
          
                
            
                        
          • 
                            
            1．某科研機構為了了解氣溫對蘑菇產量的影響，隨機抽取了某蘑菇種植大棚12月份中5天的日產量y（單位：kg）與該地當日的平均氣溫x（單位：℃）的數據，得到如圖散點圖：
            其中A（3，2），B（5，10），C（8，11），D（9，13），E（10，14）．
            （1）求出y關于x的線性回歸方程；
            （2）若該地12月份某天的平均氣溫為6℃，用（1）中所求的回歸方程預測該蘑菇種植大棚當日的產量．
            附：線性回歸直線方程
            ?
            y
            =
            ?
            b
            x
            +
            ?
            a
            中，
            ?
            b
            =
            n
            ∑
            i
            =
            1
            x
            i
            y
            i
            -
            n
            x
            y
            n
            ∑
            i
            =
            1
            x
            2
            i
            -
            n
            x
            2
            ，
            ?
            a
            =
            y
            -
            ?
            b
            x
            ．
            發布：2024/12/29 11:30:2組卷：104引用：3難度：0.7
            
                        
            • 
                        
          • 
                            
            2．某農科所對冬季晝夜溫差（最高溫度與最低溫度的差）大小與某反季節大豆新品種一天內發芽數之間的關系進行了分析研究，他們分別記錄了12月1日至12月6日每天晝夜最高、最低的溫度（如圖1），以及實驗室每天每100顆種子中的發芽數情況（如圖2），得到如下資料：
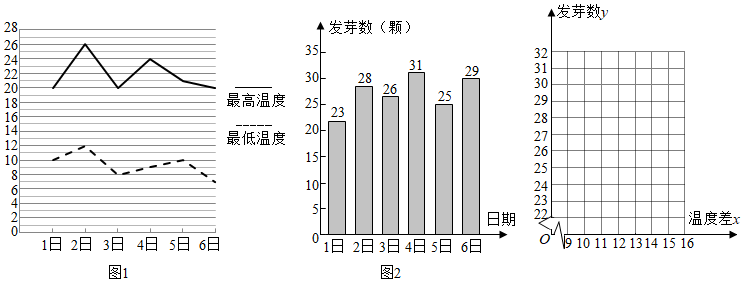
            （1）請畫出發芽數y與溫差x的散點圖；
            （2）若建立發芽數y與溫差x之間的線性回歸模型，請用相關系數說明建立模型的合理性；
            （3）①求出發芽數y與溫差x之間的回歸方程
            ?
            y
            =
            ?
            a
            +
            ?
            b
            x
            （系數精確到0.01）；
            ②若12月7日的晝夜溫差為8℃，通過建立的y關于x的回歸方程，估計該實驗室12月7日當天100顆種子的發芽數．
            參考數據：
            6
            ∑
            i
            =
            1
            x
            i
            =
            75
            ，
             
            6
            ∑
            i
            =
            1
            y
            i
            =
            162
            ，
            6
            ∑
            i
            =
            1
            x
            i
            y
            i
            =2051，
            6
            ∑
            i
            =
            1
            x
            i
            2
            -
            6
            x
            2
            ≈4.2，
            6
            ∑
            i
            =
            1
            y
            i
            2
            -
            6
            y
            2
            ≈6.5．
            參考公式：
            相關系數：r=
            n
            ∑
            i
            =
            1
            x
            i
            y
            i
            -
            n
            x
            ?
            y
            （
            n
            ∑
            i
            =
            1
            x
            i
            2
            -
            n
            x
            2
            ）
            （
            n
            ∑
            i
            =
            1
            y
            i
            2
            -
            n
            y
            2
            ）
            （當|r|＞0.75時，具有較強的相關關系）．
            回歸方程
            ?
            y
            =
            ?
            a
            +
            ?
            b
            x
            中斜率和截距計算公式：
            ?
            b
            =
            n
            ∑
            i
            =
            1
            x
            i
            y
            i
            -
            n
            x
            ?
            y
            n
            ∑
            i
            =
            1
            x
            i
            2
            -
            n
            x
            2
            ，
            ?
            a
            =
            y
            -
            ?
            b
            x
            ．
            發布：2024/12/29 12:0:2組卷：188引用：5難度：0.5
            
                        
            • 
                        
          • 
                            
            3．兩個線性相關變量x與y的統計數據如表：
            
  
    
            
      x
      9
      9.5
      10
      10.5
      11
    
            
    
            
      y
      11
      10
      8
      6
      5
    
            
              

            其回歸直線方程是
            ?
            y
            =
            ?
            b
            x+40，則相應于點（9，11）的殘差為 
            ．
            發布：2024/12/29 12:0:2組卷：115引用：8難度：0.7
            
                        
            • 
                
          
            
          
    
          
        

          

        
          
    
          
    
           
        
          APP開發者：深圳市菁優智慧教育股份有限公司| 應用名稱：菁優網 | 應用版本：5.0.7 |隱私協議|第三方SDK|用戶服務條款
          本網部分資源來源于會員上傳，除本網組織的資源外，版權歸原作者所有，如有侵犯版權，請立刻和本網聯系并提供證據，本網將在三個工作日內改正