2020-2021學年青海省海南州高級中學、貴德中學高二（下）期中數學試卷（文科）

一、選擇題：本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．若復數z=[（a²-1）i+（a-1）]i為純虛數，a∈R，則a=（　　）

  A．1

  B．-1

  C．±1

  D．0
  組卷：4引用：1難度：0.8

  解析

• 2．已知點M的極坐標為

  （

  3

  ，-

  5

  π

  3

  ）

  ，下列所給出的四個坐標中能表示點M極坐標的是（　　）

  A． （ 3 ，- π 3 ）

  B． （ 3 ， 4 π 3 ）

  C． （ 3 ，- 2 π 3 ）

  D． （ 3 ， π 3 ）
  組卷：22引用：1難度：0.5

  解析

• 3．曲線f（x）=x²-sinx在點（0，f（0））處的切線方程為（　　）

  A．y=-x

  B．y=-2x

  C． y = - 1 2 x

  D． y = - 1 3 x
  組卷：468引用：7難度：0.7

  解析

• 4．觀察如圖圖形規律，在其左下角的空格內畫上合適的圖形為（　　）
  

  	●	▲
  ▲		〇
  	△

  A．

  B．△

  C．

  D．●
  組卷：5引用：1難度：0.7

  解析

• 5．下列函數中，存在極值的函數為（　　）

  A．y=ex

  B．y=lnx

  C． y = 2 x

  D．y=x2-2x
  組卷：68引用：8難度：0.6

  解析

• 6．在極坐標系中，與圓ρ=4sinθ相切的一條直線的方程為（　　）

  A．ρcosθ=2	B．ρsinθ=2
  C．ρsin（θ+ π 3 ）=4	D．ρsin（θ- π 3 ）=4
  組卷：211引用：4難度：0.5

  解析

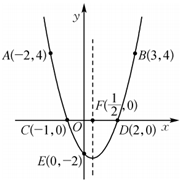• 7．如圖是函數y=f（x）（x∈R）的導函數y=f'（x）的函數圖象，則下列關于函數y=f（x）的說法正確的是（　　）

  A．函數y=f（x）的減區間為 （ - ∞ ， 1 2 ） ，增區間為 （ 1 2 ， + ∞ ）

  B．函數y=f（x）在點（-2，f（-2））和點（3，f（3））處的切線斜率相等

  C．f'（0）=2

  D．函數f（x）只有一個極小值點，沒有極大值點
  組卷：27引用：4難度：0.5

  解析

三、解答題：本大題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．

• 21．共享單車是指企業在校園、地鐵站點、公交站點、居民區、商業區、公共服務區等提供自行車單車共享服務，是共享經濟的一種新形態．一個共享單車企業在某個城市就“一天中一輛單車的平均成本（單位：元）與租用單車的數量（單位：千輛）之間的關系”進行調查研究，在調查過程中進行了統計，得出相關數據見下表：

  租用單車數量x（千輛）	2	3	4	5	8
  每天一輛車平均成本y（元）	3.2	2.4	2	1.9	1.7

  根據以上數據，研究人員分別借助甲、乙兩種不同的回歸模型，得到兩個回歸方程，方程甲：

  ?

  y

  ^（1）=

  4

  x

  +1.1，方程乙：

  ?

  y

  ^（2）=

  6

  .

  4

  x

  2

  +1.6．
  （1）為了評價兩種模型的擬合效果，完成以下任務：
  ①完成下表（計算結果精確到0.1）（備注：

  ?

  e

  i

  =y_i-

  ?

  y

  i

  ，

  ?

  e

  i

  稱為相應于點（x_i，y_i）的殘差（也叫隨機誤差）；

  租用單車數量x（千輛）		2	3	4	5	8
  每天一輛車平均成本y（元）		3.2	2.4	2	1.9	1.7
  模型甲	估計值 ? y i （1）		2.4	2.1		1.6
  	殘差 ? e i （1）		0	-0.1		0.1
  模型乙	估計值 ? y i （2）		2.3	2	1.9
  	殘差 ? e i （2）		0.1	0	0

  ②分別計算模型甲與模型乙的殘差平方和Q₁及Q₂，并通過比較Q₁，Q₂的大小，判斷哪個模型擬合效果更好．
  （2）這個公司在該城市投放共享單車后，受到廣大市民的熱烈歡迎，共享單車常常供不應求，于是該公司研究是否增加投放．根據市場調查，這個城市投放8千輛時，該公司平均一輛單車一天能收入8.4元；投放1萬輛時，該公司平均一輛單車一天能收入7.6元．問該公司應該投放8千輛還是1萬輛能獲得更多利潤？（按（1）中擬合效果較好的模型計算一天中一輛單車的平均成本，利潤=收入-成本）．
  組卷：263引用：3難度：0.1

  解析

• 22．已知函數f（x）=x+（1-a）lnx+

  a

  x

  （a∈R）．
  （1）討論函數f（x）的單調性；
  （2）當a＞0時，若f（x）≥2恒成立，求實數a的取值范圍．
  組卷：199引用：6難度：0.4

  解析