背景資料：在已知△ABC所在平面上求一點P，使它到三角形的三個頂點的距離之和最小．這個問題是法國數學家費馬1640年前后向意大利物理學家托里拆利提出的，所求的點被人們稱為“費馬點”．如圖1，當△ABC三個內角均小于120°時，費馬點P在△ABC內部，當∠APB=∠APC=∠CPB=120°時，則PA+PB+PC取得最小值．
（1）如圖2，等邊△ABC內有一點P，若點P到頂點A、B、C的距離分別為3，4，5，求∠APB的度數，為了解決本題，我們可以將△APB繞頂點A旋轉到△ACP'處，此時△ACP'≌△ABP這樣就可以利用旋轉變換，將三條線段PA、PB、PC轉化到一個三角形中，從而求出∠APB=150°150°；
知識生成：怎樣找三個內角均小于120°的三角形的費馬點呢？為此我們只要以三角形一邊在外側作等邊三角形并連接等邊三角形的頂點與△ABC的另一頂點，則連線通過三角形內部的費馬點．請同學們探索以下問題．
（2）如圖3，△ABC三個內角均小于120°，在△ABC外側作等邊三角形△ABB'，連接CB'，求證：CB'過△ABC的費馬點．
（3）如圖4，在Rt△ABC中，∠C=90°，AC=1，∠ABC=30°，點P為△ABC的費馬點，連接AP、BP、CP，求PA+PB+PC的值．
【考點】三角形綜合題．
【答案】150°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/25 8:0:9組卷：1615引用：4難度：0.1
相似題
-
1．如圖1，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，動點P在線段BC上，點Q在線段AB上，且PQ=BQ，延長QP交射線AC于點D．
（1）求證：QA=QD；
（2）設∠BAP=α，當2tanα是正整數時，求PC的長；
（3）作點Q關于AC的對稱點Q′，連接QQ′，AQ′，DQ′，延長BC交線段DQ′于點E，連接AE，QQ′分別與AP，AE交于點M，N（如圖2所示）．若存在常數k,滿足k?MN=PE?QQ′，求k的值．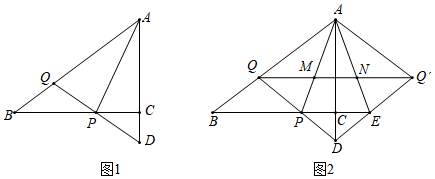
發布：2025/6/16 4:0:2組卷：233引用：3難度：0.2 -
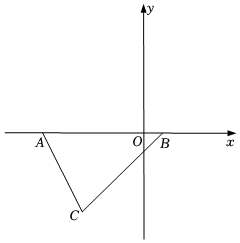2．如圖，在平面直角坐標系中，A（a,0），B（b,0），且滿足，C在第三象限，坐標為（n+1，n），連接AC，BC，（a+5）2+b-1=0
（1）請直接寫出：a=，b=，AB=，S△ABC=（用含n的代數式表示）；
（2）在線段AB上取一點D，連接CD并延長，交y軸于點E，連接AE，BE，
①若S△DCA=2S△DEA，求點E坐標，用含n的代數式表示．
②若S△ADC=S△DBE，求點E坐標．發布：2025/6/15 14:0:2組卷：144引用：1難度：0.1 -
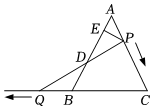3．如圖，△ABC是邊長為6的等邊三角形，P是AC邊上一動點，由A向C運動（與A，C不重合），Q是CB延長線上一點，由B向CB延長線方向運動（Q不與B重合），連接PQ交AB于D，過P作PE⊥AB于E．若兩點同時出發，以相同的速度每秒1個單位運動，運動時間為t.
（1）當∠PQC=30°時，求t的值；
（2）求證：PD=DQ；
（3）當P，Q在運動過程中線段ED的長是否發生變化？如果不變，求出線段ED的長；如果變化請說明理由．發布：2025/6/15 6:30:1組卷：151引用：1難度：0.4