【問題提出】n個m邊形最多可以把平面分成幾部分?
【問題探究】為了探究規(guī)律,我們先從最簡單的情形入手,從中找到解決問題的方法,最后得出一般性的結論.
探究一:n條直線最多可以把平面分成幾部分?
| n的數(shù)量 | 思考方式 | 結果與算式 |
| 1條直線 | 2個區(qū)域 | |
| 2條直線 | 要使分成的區(qū)域盡最多,則第2條直線要與第1條直線相交可以將平面分成4個區(qū)域; | 1+1+2=4個區(qū)域; |
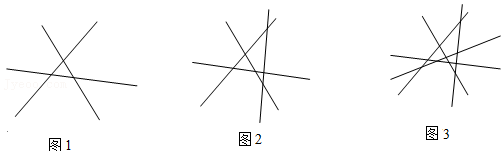
| 3條直線 | 如圖1,將第3條直線與前面2條直線盡可能兩兩相交,這樣就會得到2個交點,這2個交點將第3條直線分為了2條射線和1條線段,這樣就多了2+1=3個區(qū)域,所以3條直線至多將平面分成7個區(qū)域; | 1+1+2+3=7個區(qū)域; |
| 4條直線 | 如圖2,4條直線時,如圖2,將第4條直線與前面3條相交直線盡可能兩兩相交,這樣就會得到3個交點,這3個交點將第4條直線分為了2條射線和4-2=2條線段,這樣就多了2+2=4個區(qū)域,所以三條直線至多將平面分成11個區(qū)域; | 1+1+2+3+4=11個區(qū)域; |
結論:n條直線最多可以把平面分成
(n2+n+1)
1
2
1
2
(n2+n+1)
部分.1
2
1
2
探究二:n個圓最多可以把平面分成幾部分?
| n的數(shù)量 | 思考方式 | 結果與算式 |
| 1個圓 | 2 | |
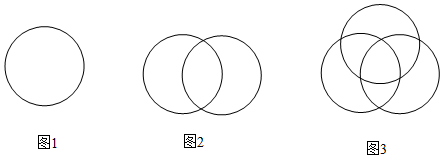
| 2個圓 | 為了使分成的區(qū)域最多,應使新增加的圓與前1個圓有2個交點,將新增加的圓分成2部分,從而增加2個區(qū)域,所以,用2個圓最多能把平面分成4個區(qū)域. | 2+2×1=4個區(qū)域 |
| 3個圓 | 為了使分成的區(qū)域最多,應使新增加的圓與前2個圓分別有2個交點,將新增加的圓分成2×2=4部分,從而增加4個區(qū)域,所以,用3個圓最多能把平面分成8個區(qū)域. | 2+2×1+2×2=8個區(qū)域 |
仿照前面的探究方法,寫出解答過程并且畫出相應的圖.
結論:n個圓最多可以把平面分成
(n2-n+2)
(n2-n+2)
部分.探究三:n個三角形最多可以把平面分成幾部分?
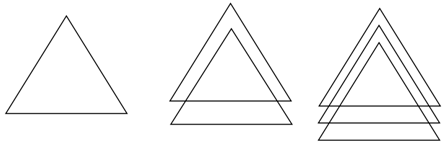
由上面的分析,當畫第n(n≥2)個三角形時,每條邊最多與前面已畫的(n-1)個三角形的各兩條邊相交,對于每個三角形,因為1條直線最多與三角形的2條邊相交,所以第n個三角形的每條邊最多與前面(n-1)個三角形的各
2
2
條邊相交,共可產生 (n2-n)
(n2-n)
(個)交點,即增加 (n2-n)
(n2-n)
部分.【一般規(guī)律】
n個四邊形最多可以把平面分成
(4n2-4n+2)
(4n2-4n+2)
部分;n個m邊形最多可以把平面分成
(4n2-4n+m-2)
(4n2-4n+m-2)
部分.【答案】(n2+n+1);(n2-n+2);2;(n2-n);(n2-n);(4n2-4n+2);(4n2-4n+m-2)
1
2
1
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網所有,未經書面同意,不得復制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:116引用:1難度:0.3
相似題
-
1.如圖,將一條長度為1的線段三等分,然后取走其中的一份,稱為第一次操作;再將余下的每一條線段三等分,然后取走其中一份,稱為第二次操作;…如此重復操作,當?shù)趎次操作結束時,被取走的所有線段長度之和為.
 發(fā)布:2025/5/25 21:0:1組卷:829引用:45難度:0.7
發(fā)布:2025/5/25 21:0:1組卷:829引用:45難度:0.7 -
2.如圖,將大小相同的小圓規(guī)律擺放:第1個圖形有5個小圓,第2個圖形有8個小圓,第3個圖形有11個小圓,…依此規(guī)律,第n個圖形的小圓個數(shù)是 個.
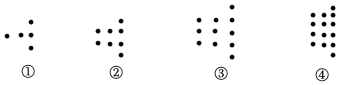 發(fā)布:2025/5/25 17:30:1組卷:65引用:2難度:0.5
發(fā)布:2025/5/25 17:30:1組卷:65引用:2難度:0.5 -
3.如圖是一組有規(guī)律的圖案,它們是由邊長相同的小正方形組成,其中部分小正方形涂有陰影,依此規(guī)律,第10個圖案中涂有陰影的小正方形的個數(shù)為( )
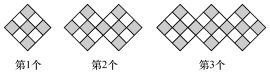
A.50 B.45 C.41 D.36 發(fā)布:2025/5/25 19:30:2組卷:652引用:4難度:0.6


