2019年山東省青島市市南區中考數學一模試卷

一、選擇題。（本題滿分24分，共有8道小題，每小題3分）下列每小題都給出標號為A.B.C.D的四個結論，其中只有一個是正確的，每小題選對得分，不選、錯選或選出的標號超過一個的不得分。

• 1．“低碳環保”入人心，共享單車已成出行新方式，下列圖標中，是軸對稱的是（　　）

  A．

  B．

  C．

  D．
  組卷：224引用：5難度：0.8

  解析

• 2．如圖所示的物體的左視圖是（　　）

  A．

  B．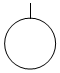

  C．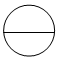

  D．
  組卷：115引用：4難度：0.8

  解析

• 3．下列四個數中，其絕對值小于2的數是（　　）

  A．-3

  B． 5

  C．-π

  D．- 2
  組卷：185引用：5難度：0.9

  解析

• 4．國家統計局12月6日發布數據，2021年全國糧食產量再創新高，總產達13657億斤，比上年增長2.0%，連續7年保持在1.3萬億斤以上．13657億斤即1365700000000斤，把1365700000000用科學記數法表示為（　　）

  A．13.657×1011	B．1.3657×1012
  C．0.13657×1013	D．1.3657×1011
  組卷：187引用：3難度：0.7

  解析

• 5．一個密閉不透明的盒子里有若干個白球，在不允許將球倒出來的情況下，為估計白球的個數，小剛向其中放入8個黑球，搖勻后從中隨機摸出一個球記下顏色，再把它放回盒中，不斷重復，共摸球400次，其中88次摸到黑球，估計盒中大約有白球（　　）

  A．28個

  B．30個

  C．36個

  D．42個
  組卷：1015引用：60難度：0.7

  解析

• 6．不等式組

  x + 3 ＞ 1

  - 3 x ≥ - 3

  的解集在數軸上表示正確的是（　　）

  A．	B．
  C．	D．
  組卷：507引用：5難度：0.6

  解析

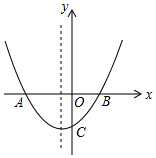• 7．已知拋物線y=ax²+bx+c交x軸于點B （1，0）和點A，交y軸負半軸于點C，且AO=2CO．有下列結論：①2b+2c=-1；②a=

  1

  2

  ；③

  a

  +

  2

  b

  c

  ＞0；④4ac+2b+1=0．其中，正確結論的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：1456引用：4難度：0.4

  解析

• 8．如圖，在邊長為1的正方形ABCD中，E、F是AD邊上的兩個動點，且AE=FD，連接BE、CF、BD，CF與BD交于點G，連接AG交BE于點H，連接DH，下列結論正確的個數是（　　）
  ①AG⊥BE；②HD平分∠EHG；③△ABG∽△FDG；④S_△HDG：S_△HBG=tan∠DAG；⑤線段DH的最小值是

  5

  -

  1

  2

  ；⑥當E、F重合時，延長AG交CD于M，則tan∠EBM=

  3

  4

  ．

  A．5個

  B．4個

  C．3個

  D．2個
  組卷：766引用：4難度：0.2

  解析

四、解答題。（本題滿分74分，共有9道小題）

• 23．【問題提出】n個m邊形最多可以把平面分成幾部分？
  【問題探究】為了探究規律，我們先從最簡單的情形入手，從中找到解決問題的方法，最后得出一般性的結論．
  探究一：n條直線最多可以把平面分成幾部分？
  

  n的數量	思考方式	結果與算式
  1條直線		2個區域
  2條直線	要使分成的區域盡最多，則第2條直線要與第1條直線相交可以將平面分成4個區域；	1+1+2=4個區域；
  3條直線	如圖1，將第3條直線與前面2條直線盡可能兩兩相交，這樣就會得到2個交點，這2個交點將第3條直線分為了2條射線和1條線段，這樣就多了2+1=3個區域，所以3條直線至多將平面分成7個區域；	1+1+2+3=7個區域；
  4條直線	如圖2，4條直線時，如圖2，將第4條直線與前面3條相交直線盡可能兩兩相交，這樣就會得到3個交點，這3個交點將第4條直線分為了2條射線和4-2=2條線段，這樣就多了2+2=4個區域，所以三條直線至多將平面分成11個區域；	1+1+2+3+4=11個區域；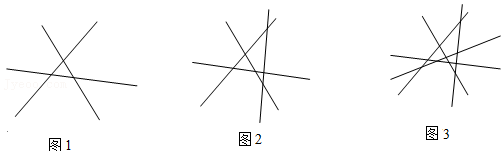

  
  結論：n條直線最多可以把平面分成

  部分．
  探究二：n個圓最多可以把平面分成幾部分？
  

  n的數量	思考方式	結果與算式
  1個圓		2
  2個圓	為了使分成的區域最多，應使新增加的圓與前1個圓有2個交點，將新增加的圓分成2部分，從而增加2個區域，所以，用2個圓最多能把平面分成4個區域．	2+2×1=4個區域
  3個圓	為了使分成的區域最多，應使新增加的圓與前2個圓分別有2個交點，將新增加的圓分成2×2=4部分，從而增加4個區域，所以，用3個圓最多能把平面分成8個區域．	2+2×1+2×2=8個區域

  用4個圓最多能把平面分成幾個區域？
  仿照前面的探究方法，寫出解答過程并且畫出相應的圖．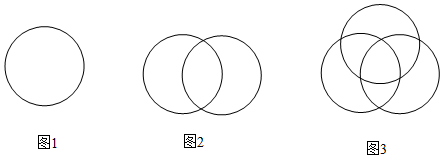
  
  結論：n個圓最多可以把平面分成

  部分．
  探究三：n個三角形最多可以把平面分成幾部分？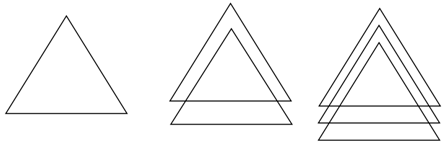
  
  由上面的分析，當畫第n（n≥2）個三角形時，每條邊最多與前面已畫的（n-1）個三角形的各兩條邊相交，對于每個三角形，因為1條直線最多與三角形的2條邊相交，所以第n個三角形的每條邊最多與前面（n-1）個三角形的各

  條邊相交，共可產生

  （個）交點，即增加

  部分．
  【一般規律】
  n個四邊形最多可以把平面分成

  部分；
  n個m邊形最多可以把平面分成

  部分．
  組卷：116引用：1難度：0.3

  解析

• 24．如圖，在矩形ABCD中，AB=3，BC=4，動點P從點D出發沿DA向終點A運動，同時動點Q從點A出發沿對角線AC向終點C運動．過點P作PE∥DC，交AC于點E，動點P、Q的運動速度是每秒1個單位長度，當點P運動到點A時，P、Q兩點同時停止運動．設運動時間為t s（0≤t≤6），解答下列問題：
  （1）當B、E、D共線時，求t的值；
  （2）設四邊形BQPE的面積為S，當線段PE在點Q右側時，求出S與t之間的函數關系式；
  （3）當BE∥PQ時，求t的值；
  （4）是否存在這樣的點P和點Q，使P、Q、E為頂點的三角形是等腰三角形？若存在，請求出所有滿足要求的t的值；若不存在，請說明理由．
  組卷：341引用：2難度：0.2

  解析