【問題呈現】阿基米德折弦定理：
如圖1，AB和BC是⊙O的兩條弦（即折線ABC是圓的一條折弦），BC＞AB，點M是?ABC的中點，則從M向BC所作垂線的垂足D是折弦ABC的中點，即CD=DB+BA．下面是運用“截長法”證明CD=DB+BA的部分證明過程．
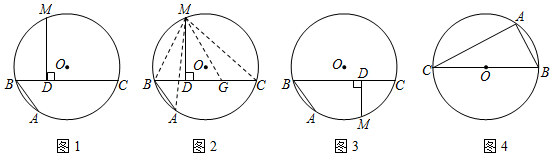
證明：如圖2，在CD上截取CG=AB，連接MA、MB、MC和MG．
∵M是?ABC的中點，
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根據證明過程，分別寫出下列步驟的理由：
①相等的弧所對的弦相等相等的弧所對的弦相等，
②同弧所對的圓周角相等同弧所對的圓周角相等，
③有兩組邊及其夾角分別對應相等的兩個三角形全等有兩組邊及其夾角分別對應相等的兩個三角形全等；
【理解運用】如圖1，AB、BC是⊙O的兩條弦，AB=4，BC=6，點M是?ABC的中點，MD⊥BC于點D，則BD=11；
【變式探究】如圖3，若點M是?AC的中點，【問題呈現】中的其他條件不變，判斷CD、DB、BA之間存在怎樣的數量關系？并加以證明．
【實踐應用】根據你對阿基米德折弦定理的理解完成下列問題：
如圖4，BC是⊙O的直徑，點A圓上一定點，點D圓上一動點，且滿足∠DAC=45°，若AB=6，⊙O的半徑為5，求AD長．
?
ABC
?
ABC
?
ABC
?
AC
【考點】圓的綜合題．
【答案】相等的弧所對的弦相等；同弧所對的圓周角相等；有兩組邊及其夾角分別對應相等的兩個三角形全等；1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/8 8:0:9組卷：958引用：3難度：0.3
相似題
-
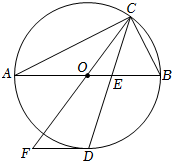1．如圖，點C在以AB為直徑的⊙O上，CD平分∠ACB交⊙O于點D，交AB于點E，過點D作⊙O的切線交CO的延長線于點F．
（1）求證：FD∥AB；
（2）若AC=2，BC=5，求FD的長．5發布：2025/5/23 0:30:1組卷：2147引用：13難度：0.2 -
2．已知：四邊形ABCD內接于⊙O，AC、BD即相交于點F，連接OC，∠BCO=∠ABD．
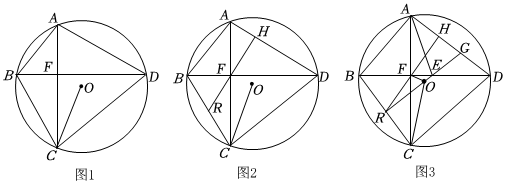
（1）如圖1，求證：AC⊥BD；
（2）如圖2，過點F作FH⊥AD于點H，延長HF交BC于點R．求證：BR=CR；
（3）如圖3，在（2）的條件下，點E、點G分別是FD，AD上的點，連接AE、EG、OR，∠ADB=2∠CAE，，EF=2，EG=DG=154，求⊙O的半徑．tan∠FOR=76發布：2025/5/22 23:30:1組卷：131引用：1難度：0.3 -
3．在平面直角坐標系xOy中，已知點M（a,b），N．
對于點P給出如下定義：將點P向右（a≥0）或向左（a＜0）平移|a|個單位長度，再向上（b≥0）或向下（b＜0）平移|b|個單位長度，得到點P'，點P'關于點N的對稱點為P″，NP″中點記為Q，稱點Q為點P的“對應點”．
（1）如圖，點M（1，1），點N在線段OM的延長線上，若點P（-3，0），點Q為點P的“對應點”．
①在圖1中畫出點Q；
②連接PQ，交線段ON于點T．求證：；NT=13OM
（2）⊙O的半徑為2，M是⊙O上一點，點N在線段OM上，且ON=t（1＜t＜2），若P為⊙O外一點，點Q為點P的“對應點”，連接PQ．當點M在⊙O上運動時，直接寫出PQ長的最大值與最小值的差（用含t的式子表示）．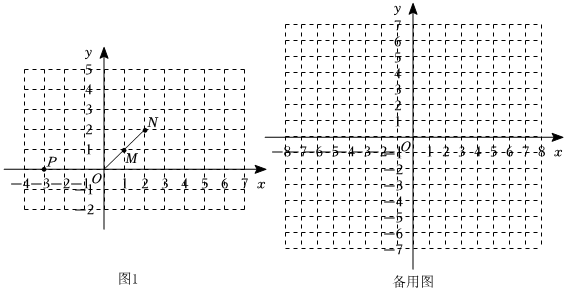
發布：2025/5/23 0:0:1組卷：176引用：1難度：0.3