已知：在△ABC中，點E在直線AC上，點B、D、E在同一條直線上，且BA=BD，∠BAE=∠D．
（1）如圖1，若BE平分∠ABC，求證：∠AEB+∠BCE=180°．
（2）如圖2，若BE平分∠ABC的外角∠ABF，交CA的延長線于點E，問：∠AEB和∠BCE的數量關系發生改變了嗎？若改變，請寫出正確的結論，并證明；若不改變，請說明理由．
（3）如圖3，在（2）的條件下，若AB⊥BC，CD=1，求EC的長度．
【考點】三角形綜合題．
【答案】（1）證明見解析過程；
（2）結論改變，∠AEB=∠BCE，理由見解析過程；
（3）1+．
（2）結論改變，∠AEB=∠BCE，理由見解析過程；
（3）1+
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：76引用：1難度：0.1
相似題
-
1．下面是某數學興趣小組探究用不同方法作一條線段的垂直平分線的討論片段，請仔細閱讀，并完成相應任務．
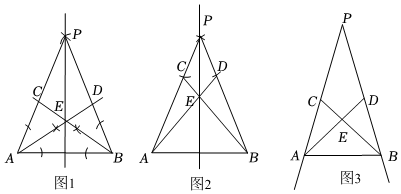
小晃：如圖1，（1）分別以A，B為圓心，大于 AB為半徑作弧，兩弧交于點P；（2）分別作∠PAB，∠PBA的平分線AD，BC，交點為E；（3）作直線PE．直線PE即為線段AB的垂直平分線．12
簡述作圖理由：
由作圖可知，PA=PB，所以點P在線段AB的垂直平分線上，∠PAB=∠PBA，因為AD，BC分別是∠PAB，∠PBA的平分線，所以∠DAB=∠CBA，所以AE=BE，所以點E在線段AB的垂直平分線上，所以PE是線段AB的垂直平分線．
小航：我認為小晃的作圖方法很有創意，但是可以改進如下，如圖2，（1）分別以A，B為圓心，大于AB為半徑作弧，兩弧交于點P；（2）分別在線段PA，PB上截取PC=PD；（3）連接AD，BC，交點為E；（4）作直線PE．直線PE即為線段AB的垂直平分線．12
…
任務：
（1）小晃得出點P在線段AB的垂直平分線上的依據是 ；
（2）小航作圖得到的直線PE是線段AB的垂直平分線嗎？請判斷并說明理由；
（3）如圖3，已知∠P=30°，PA=PB，AB=，點C，D分別為射線PA，PB上的動點，且PC=PD，連接AD，BC，交點為E，當AD⊥BC時，請直接寫出線段AC的長．6發布：2025/6/9 17:0:1組卷：489引用：6難度：0.3 -
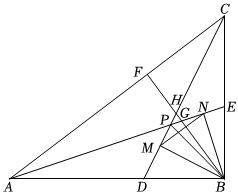2．如圖，在直角三角形ABC中，∠ABC=90°，AB=8，BC=6，∠CAB和∠ACB的角平分線AE，CD交于點P，AC邊上的高BF與AE、CD分別交于點G、H，M、N分別為DH、EG的中點，連接MN、BM、BN，下列說法正確的是 ．
①BF=4.8，
②△ABP與△CBP的面積之比為3：4，
③△BDH為等腰三角形，
④BN⊥AE，
⑤∠MNP=∠EAB（請填入相應的序號）．發布：2025/6/9 16:0:2組卷：160引用：1難度：0.4 -
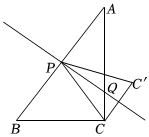3．在Rt△ABC中，∠C=90°，AC=4，BC=3，動點P從點A出發，以每秒4個單位長度的速度向終點B運動．過點P作PQ⊥AB交折線AC-CB于點Q，作點C關于直線PQ的對稱點C'．設點P的運動時間為t（t＞0）．
（1）用含t的代數式表示線段PQ的長；
（2）當點Q在線段AC上時，設直線PQ與直線BC交于點M，當△APQ和△QCM全等時，求t的值；
（3）當△PCC'為等邊三角形時，直接寫出滿足條件的t值；
（4）當點C'和△ABC的某兩個頂點距離相等時，直接寫出滿足條件的t值．發布：2025/6/9 16:0:2組卷：111引用：1難度：0.2