在數學中,布勞威爾不動點定理是拓撲學里一個非常重要的不動點定理,得名于荷蘭數學家魯伊茲?布勞威爾(L.EJ.Brouwer),簡單的講就是對于滿足一定條件的圖象不間斷的函數f(x),存在一個點x0,使得f(x0)=x0,那么我們稱該函數為“不動點”函數.下列函數為“不動點”函數的是( )
f ( x ) = - 1 x | |
h ( x ) = x 2 + 4 + x + 3 | φ ( x ) = 1 x - x |
【考點】函數的概念及其構成要素.
【答案】D
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/10/12 9:0:2組卷:57引用:1難度:0.7
相似題
-
1.設M={x|0≤x≤2},N={y|0≤y≤2},給出下列四個圖形:
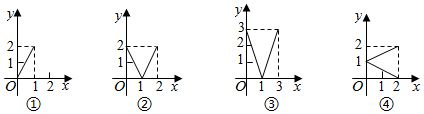
其中,能表示從集合M到集合N的函數關系的個數是( )A.0 B.1 C.2 D.3 發布:2024/12/17 2:30:1組卷:864引用:13難度:0.9 -
2.德國著名數學家狄利克雷(Dirichlet,1805~1859)在數學領域成就顯著,19世紀,狄利克雷定義了一個“奇怪的函數”y=f(x)=
,其中R為實數集,Q為有理數集.則關于函數f(x),有如下四個命題,其中真命題的是( )1,x∈Q0,x∈?RQA.函數f(x)不是偶函數 B.?x1,x2∈?RQ,f(x1+x2)=f(x1)+f(x2)恒成立 C.任取一個不為零的有理數T,f(x+T)=f(x)任意的x∈R恒成立 D.不存在三個點A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC為等腰直角三角形 發布:2024/12/22 8:0:1組卷:43引用:1難度:0.5 -
3.可以表示以x為自變量的函數圖象是( )
A. 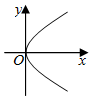
B. 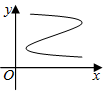
C. 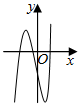
D. 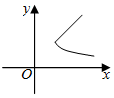 發布:2024/12/11 17:0:1組卷:964引用:6難度:0.9
發布:2024/12/11 17:0:1組卷:964引用:6難度:0.9


