閱讀下面材料：
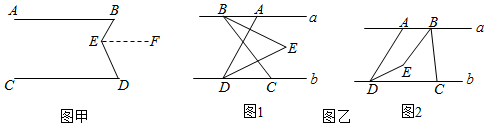
小穎遇到這樣一個問題：已知：如圖甲，AB∥CD，E為AB，CD之間一點，連接BE，DE，∠B=35°，∠D=37°，求∠BED的度數．
她是這樣做的：
過點E作EF∥AB，
則有∠BEF=∠B．
因為AB∥CD，
所以EF∥CD．①
所以∠FED=∠D．
所以∠BEF+∠FED=∠B+∠D．
即∠BED=

∠B+∠D

∠B+∠D

．
Ⅰ．小穎求得∠BED的度數為

72°

72°

；
Ⅱ．上述思路中的①的理由是

平行于同一直線的兩條直線互相平行

平行于同一直線的兩條直線互相平行

；
Ⅲ．請你參考她的思考問題的方法，解決問題：如圖乙．
已知：直線a∥b,點A，B在直線a上，點C，D在直線b上，連接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直線交于點E．
（1）如圖1，當點B在點A的左側時，若∠ABC=α，∠ADC=β，則∠BED的度數為

1

2

（α+β）．

1

2

（α+β）．

（用含有α，β的式子表示）．
（2）如圖2，當點B在點A的右側時，設∠ABC=α，∠ADC=β，直接寫出∠BED的度數（用含有α，β的式子表示）．