公元前3世紀，古希臘歐幾里得在《幾何原本》里提出：“球的體積（V）與它的直徑（D）的立方成正比”，此即V=kD3，歐幾里得未給出k的值.17世紀日本數學家們對求球的體積的方法還不了解，他們將體積公式V=kD3中的常數k稱為“立圓率”或“玉積率”．類似地，對于等邊圓柱（軸截面是正方形的圓柱）、正方體也可利用公式V=kD3求體積（在等邊圓柱中，D表示底面圓的直徑；在正方體中，D表示棱長）．假設運用此體積公式求得球（直徑為a）、等邊圓柱（底面圓的直徑為a）、正方體（棱長為a）的“玉積率”分別為k1、k2、k3，那么k1：k2：k3（ ）
【考點】類比推理．
【答案】D
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：221引用：7難度：0.7
相似題
-
1．若
，x≠kπ+π4，則y=tanx的周期為π．類比可推出：設x∈R且tan（x+π4）=1+tanx1-tanx，則y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）發布：2025/1/6 8:0:1組卷：36引用：1難度：0.5 -
2．已知
tan（x+π4）=1+tanx1-tanx，那么函數y=tanx的周期為π．類比可推出：已知x∈R且（x≠kπ+π4），那么函數y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）發布：2025/1/6 8:0:1組卷：11引用：1難度：0.7 -
3．閱讀下表后，請應用類比的思想，得出橢圓中的結論：
圓 橢圓 定
義平面上到動點P到定點O的距離等于定長的點的軌跡 平面上的動點P到兩定點F1，F2的距離之和等于定值2a的點的軌跡（2a＞|F1F2|） 結
論如圖，AB是圓O的直徑，直線AC，BD是圓O過A，B的切線，P是圓O上任意一點，
CD是過P的切線，則有“PO2=PC?PD”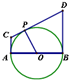
橢圓的長軸為AB，O是橢圓的中心，F1，F2是橢圓的焦點，直線AC，BD是橢圓過A，B的切線，P是橢圓上任意一點，CD是過P的切線，則有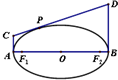 
發布：2025/1/28 8:0:2組卷：32引用：2難度：0.5