已知，△ABC中，AB=6，AB邊上的高為4．
（1）如圖1，四邊形EFGH為正方形，E、F在邊AB上，G、H分別在邊AC、BC上．求正方形的邊長；
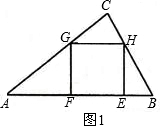
（2）如圖2，三角形內(nèi)有并排的兩個全等的正方形，它們組成的矩形DEFG的頂點D、E在△ABC的邊AB上，G、F分別在邊AC、BC上．正方形的邊長為127127；
（3）如圖3，三角形內(nèi)有并排的三個全等的正方形，它們組成的矩形有兩個頂點在△ABC的邊AB上，其它頂點分別在邊AC、BC上．正方形的邊長為4343；
（4）如圖4，三角形內(nèi)有并排的n個全等的正方形，它們組成的矩形的兩個頂點在△ABC的邊AB上，其它頂點分別在邊AC、BC上．正方形的邊長用含n的代數(shù)式表示122n+3122n+3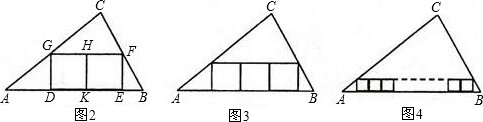
12
7
12
7
4
3
4
3
12
2
n
+
3
12
2
n
+
3
【考點】正方形的性質；相似三角形的判定與性質．
【答案】；；
12
7
4
3
12
2
n
+
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：158引用：2難度：0.1
相似題
-
1．如圖，已知正方形ABCD的邊長為6，點E，F(xiàn)分別在邊AB，BC上，BE=CF=2，CE與DF交于點H，點G為DE的中點，連接GH，則GH的長為（ ）發(fā)布：2024/12/23 20:0:2組卷：893引用：5難度：0.3 -
2．閱讀下面的例題及點撥，并解決問題：
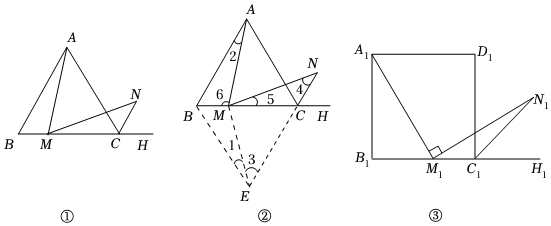
如圖①，在等邊△ABC中，M是BC邊上一點（不含端點B，C），N是△ABC的外角∠ACH的平分線上一點，且AM=MN．求證：∠AMN=60°．
（1）點撥：如圖②，作∠CBE=60°，BE與NC的延長線相交于點E，得等邊△BEC，連接EM．易證：△ABM≌△EBM（SAS），請完成剩余證明過程：
（2）拓展：如圖③，在正方形A1B1C1D1中，M1是B1C1邊上一點（不含端點B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分線上一點，且A1M1=M1N1．求證：∠A1M1N1=90°．發(fā)布：2024/12/23 19:0:2組卷：2003引用：8難度：0.1 -
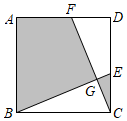3．如圖，在正方形ABCD中，AB=3，點EF分別在CD，AD上，CE=DF，BE，CF相交于點G．若圖中陰影部分的面積與正方形ABCD的面積之比為2：3，則△BCG的周長為（ ）發(fā)布：2024/12/23 19:0:2組卷：1566引用：14難度：0.8