十字測天儀廣泛應用于歐洲中世紀晚期的航海領域,主要用于測量太陽等星體的方位,便于船員確定位置.如圖1所示,十字測天儀由桿AB和橫檔CD構成,并且E是CD的中點,橫檔與桿垂直并且可在桿上滑動.十字測天儀的使用方法如下:如圖2,手持十字測天儀,使得眼睛可以從A點觀察.滑動橫檔CD使得A,C在同一水平面上,并且眼睛恰好能觀察到太陽,此時視線恰好經過點D,DE的影子恰好是AE.然后,通過測量AE的長度,可計算出視線和水平面的夾角∠CAD(稱為太陽高度角),最后通過查閱地圖來確定船員所在的位置.
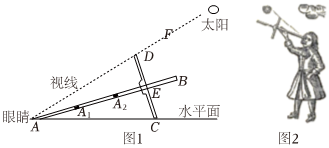
(1)若在某次測量中,橫檔CD的長度為20,測得太陽高度角∠CAD=60°,求影子AE的長;
(2)若在另一次測量中,AE=40,橫檔CD的長度為20,求太陽高度角的正弦值;
(3)在桿AB上有兩點A1,A2滿足AA1=12AA2.當橫檔CD的中點E位于Ai時,記太陽高度角為ai(i=1,2),其中α1,α2都是銳角.證明:α1<2α2.
1
2
A
A
2
【考點】解三角形.
【答案】(1)AE=10;
(2)太陽高度角的正弦值為;
(3)證明見解析.
3
(2)太陽高度角的正弦值為
8
17
(3)證明見解析.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/5 8:0:9組卷:90引用:6難度:0.5
相似題
-
1.在①
,②2a-c=2bcosC,③(a-b)(a+b)=(a-c)c這三個條件中任選一個,補充在下面的問題中,并解答該問題.3(a-bcosC)=csinB
在△ABC中,內角A,B,C的對邊分別是a,b,c,且滿足 _____,.b=23
(1)若a+c=4,求△ABC的面積;
(2)求△ABC周長l的取值范圍.發布:2024/12/29 13:0:1組卷:282引用:4難度:0.5 -
2.已知燈塔A在海洋觀察站C的北偏東65°,距離海洋觀察站C的距離為akm,燈塔B在海洋觀察站C的南偏東55°,距離海洋觀察站C的距離為3akm,則燈塔A與燈塔B的距離為( )
A.akm B. akm3C. akm7D.2akm 發布:2024/12/30 4:0:3組卷:50引用:3難度:0.7 -
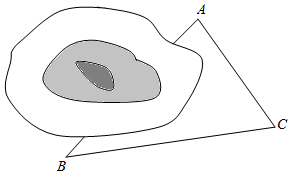 3.如圖,在鐵路建設中,需要確定隧道兩端的距離(單位:百米),已測得隧道兩端點A,B到某一點C的距離分別為5和8,∠ACB=60°,則A,B之間的距離為( )
3.如圖,在鐵路建設中,需要確定隧道兩端的距離(單位:百米),已測得隧道兩端點A,B到某一點C的距離分別為5和8,∠ACB=60°,則A,B之間的距離為( )A.7 B.10 129C.6 D.8 發布:2024/12/29 13:0:1組卷:294引用:5難度:0.7


