已知，點M是△ABC的邊BC的中點，分別以AB和AC為斜邊，向△ABC的外側畫等腰直角三角形ABD和等腰直角三角形ACE，連接MD、ME．
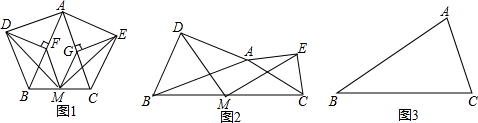
（1）如圖1，在△ABC中，AB=AC，DF⊥AB于點F，EG⊥AC于點G，連接MF、MG，求證：MF=MG，MD=ME；
（2）如圖2，△ABC是鈍角三角形，且AB≠AC，其他條件不變，那么MD=ME還成立嗎？說明理由；
（3）如圖3，在任意△ABC中，仍分別以AB和AC為斜邊，在∠BAC的內部畫等腰直角三角形ABD和等腰直角三角形ACE，M是BC的中點，連接MD、ME和DE，請在圖3中畫出正確的圖形，并直接寫出△MED的形狀．
【考點】三角形綜合題．
【答案】（1）證明過程見解答；
（2）MD=ME成立，理由見解答；
（3）圖形見解答；△DME為等腰直角三角形．
（2）MD=ME成立，理由見解答；
（3）圖形見解答；△DME為等腰直角三角形．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/31 8:0:9組卷：34引用：1難度：0.1
相似題
-
1．有共同頂點的△ABC與△ADE中，CA=CB，EA=ED，且∠ACB=∠AED=α，連接BD，CE，線段BD，CE相交于點H．
（1）如圖①，當α=60°時，的值是 ，∠BHC的度數是 ；BDCE
（2）如圖②，當α=90°時，求的值和∠BHC的度數，并說明理由；BDCE
（3）如果α=90°，=2，當點H與△ADE的頂點重合時，請直接寫出ACAE的值．BDDE
發布：2025/6/2 2:0:16組卷：821引用：2難度：0.1 -
2．感知：如圖①，AD平分∠BAC，∠B+∠C=180°，∠B=90°，易知：DB=DC．
探究：如圖②，AD平分∠BAC，∠ABD+∠ACD=180°，∠ABD＜90°，求證：DB=DC．
應用：如圖③，四邊形ABCD中，∠B=45°，∠C=135°，DB=DC=，則AB-AC=2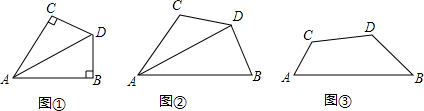
發布：2025/6/2 4:30:1組卷：421引用：3難度：0.3 -
3．已知AD是△ABC的邊BC上的高，AE平分∠BAD交BC于點E，∠C=∠B+
∠BAD．12
（1）如圖1，求證：AE=AC；
（2）如圖2，點F是AB的中點，過點A作AG∥BC交CF的延長線于點G．
①求證：AG=BE+2DE；
②如圖3，連接EG交AB于H，若AD=AH，求∠B的度數．發布：2025/6/2 3:30:1組卷：311引用：2難度：0.5