在等腰直角△ABC中，∠C=90°，AC=4，點D為射線CB上一動點（點D不與點B、C重合），以AD為腰且在AD的右側(cè)作等腰直角△ADF，∠ADF=90°，射線AB與射線FD交于點E，聯(lián)結(jié)BF．
（1）如圖所示，當點D在線段CB上時，
①求證：△ACD∽△ABF；
②設CD=x,tan∠BFD=y,求y關(guān)于x的函數(shù)解析式，并寫出x的取值范圍；
（2）當AB=2BE時，求CD的長．
【考點】相似形綜合題．
【答案】（1）①證明見解析；②y關(guān)于x的函數(shù)解析式y(tǒng)=，x的取值范圍：0＜x＜4；（2）3+．
4
-
x
4
+
x
17
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：697引用：1難度：0.3
相似題
-
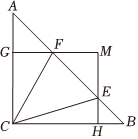1．如圖，在△ABC中，∠ACB=90°，AC=BC=1，E，F(xiàn)是線段AB上的兩個動點，且∠ECF=45°，過點E，F(xiàn)分別作BC，AC的垂線相交于點M，垂足分別為H，G．有以下結(jié)論：①AB=；②當點E與點B重合時，MH=2；③△ACE∽△BFC；④AF+BE=EF．其中正確的結(jié)論有（ ）12發(fā)布：2025/6/3 15:0:1組卷：1604引用：6難度：0.4 -
2．【基礎鞏固】
（1）如圖1，在△ABC中，D為AB上一點，∠ACD=∠B．求證：AC2=AD?AB．
【嘗試應用】
（2）如圖2，在平行四邊形ABCD中，E為BC上一點，F(xiàn)為CD延長線上一點．∠BFE=∠A，若BF=6，BE=4，求AD的長．
【拓展提高】
（3）如圖3，在菱形ABCD中，E是AB上一點，F(xiàn)是△ABC內(nèi)一點．EF∥AC，AC=2EF，∠EDF=∠BAD直接寫出線段DE與線段EF之間的數(shù)量關(guān)系．12發(fā)布：2025/6/3 12:0:1組卷：590引用：7難度：0.4 -
3．在△EFG中，∠EFG=90°，EF=FG，且點E，F(xiàn)分別在矩形ABCD的邊AB，AD上，AB=8，AD=6．
（1）如圖1，當點G在CD上時，求AE+DG的值；
（2）如圖2，F(xiàn)G與CD相交于點N，連接EN，當EF平分∠AEN時，求證：EN=AE+DN；
（3）如圖3，EG，F(xiàn)G分別交CD于點M，N，當MG2=MN?MD時，求AE的值．發(fā)布：2025/6/2 22:30:1組卷：199引用：2難度：0.3
相關(guān)試卷