綜合與實踐
綜合與實踐課上，老師讓同學(xué)們以“三角板的平移”為主題開展數(shù)學(xué)活動．
（1）操作判斷
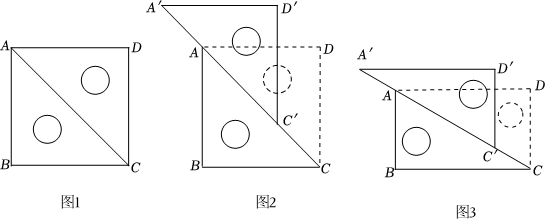
操作一：將一副等腰直角三角板兩斜邊重合，按圖1放置；
操作二：將三角板ACD沿CA方向平移（兩三角板始終接觸）至圖2位置．
根據(jù)以上操作，填空：
圖2中AA'與CC'的數(shù)量關(guān)系是 AA′=CC′AA′=CC′；四邊形ABC′D′的形狀是 平行四邊形平行四邊形；
（2）遷移探究
小航將一副等腰直角三角板換成一副含30°角的直角三角板，繼續(xù)探究，已知三角板AB邊長為6cm,過程如下：
將三角板ACD按（1）中的方式操作，如圖3，在平移過程中，四邊形ABC'D'的形狀能否是菱形，若不能，請說明理由，若能，請求出CC'的長；
（3）拓展應(yīng)用
在（2）的探究過程中，當(dāng)△BCC′為等腰三角形時，CC'的長是 6或636或63cm.
?
3
3
【考點】四邊形綜合題．
【答案】AA′=CC′；平行四邊形；6或6
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/17 8:0:9組卷：166引用：4難度：0.5
相似題
-
1．如圖，四邊形ABCD中，∠A=∠B=90°，AD=2，AB=5，BC=3．
（1）如圖①，P為AB上的一個動點，以PD，PC為邊作?PCQD．
①請問四邊形PCQD能否成為矩形？若能，求出AP的長；若不能，請說明理由．
②填空：當(dāng)AP=時，四邊形PCQD為菱形；
③填空：當(dāng)AP=時，四邊形PCQD有四條對稱軸．
（2）如圖②，若P為AB上的一點，以PD，PC為邊作?PCQD，請問對角線PQ的長是否存在最小值？若存在，請求出最小值；若不存在，請說明理由．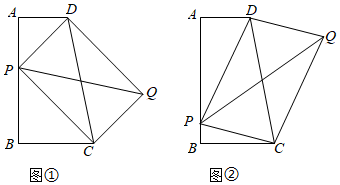
發(fā)布：2025/5/24 11:0:1組卷：701引用：3難度：0.2 -
2．綜合與實踐
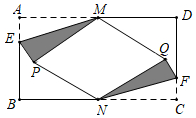
問題情境：在數(shù)學(xué)活動課上，老師讓同學(xué)們以“矩形的折疊”為主題開展數(shù)學(xué)活動如圖，矩形紙片ABCD中，點M、N分別是AD、BC的中點，點E、F分別在AB、CD上，且AE=CF．
動手操作：將△AEM沿EM折疊，點A的對應(yīng)點為點P，將△NCF沿NF折疊，點C的對應(yīng)點為點Q，點P、Q均落在矩形ABCD的內(nèi)部，連接PN、QM．
問題解決：（1）判斷四邊形PNQM的形狀，并證明；
（2）當(dāng)AD=2AB=4，四邊形PNQM為菱形時，求AE的長．發(fā)布：2025/5/24 11:30:1組卷：112引用：2難度：0.3 -
3．在四邊形ABCD中，AB=BC，∠B=60°；
（1）如圖1，已知，∠D=30°求得∠A+∠C的大小為．
（2）已知AD=3，CD=4，在（1）的條件下，利用圖1，連接BD，并求出BD的長度；
（3）問題解決；如圖2，已知∠D=75°，BD=6，現(xiàn)需要截取某種四邊形的材料板，這個材料板的形狀恰巧符合如圖2所示的四邊形，為了盡可能節(jié)約，你能求出這種四邊形面積的最小值嗎？如果能，請求出此時四邊形ABCD面積的最小值；如果不能，請說明理由．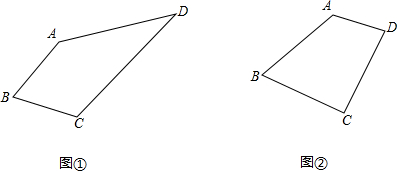
發(fā)布：2025/5/24 12:0:1組卷：527引用：3難度：0.1