閱讀下列材料，解答問(wèn)題：
材料：從等腰三角形一個(gè)頂點(diǎn)引出一條射線與對(duì)邊相交，頂點(diǎn)與交點(diǎn)之間的線段把這個(gè)三角形分割成兩個(gè)小三角形，如果分得的兩個(gè)三角形都是等腰三角形，我們把這條線段叫做三角形的完美分割線．例如：線段BM把等腰△ABC分成△ABM與△BCM（如圖1），如果△ABM與△BCM均為等腰三角形，那么線段BM叫做△ABC的完美分割線．
解答下列問(wèn)題：
（1）如圖1，已知△ABC中，AB=AC，∠BAC=36°，BM為△ABC的完美分割線，且CM＜AM，則∠C=7272°，∠AMB=108108°；
（2）如圖2，已知△ABC中，AB=AC，∠B=36°，AC=CN，求證：AN為△ABC的完美分割線；
（3）如圖3，已知△ABC是一等腰三角形紙片，AB=AC，AN是它的一條完美分割線，且BN＞NC，將△ACN沿直線AN折疊后，點(diǎn)C落在點(diǎn)C1處，AC1交BN于點(diǎn)M，求證：BM=C1N．
【考點(diǎn)】幾何變換綜合題．
【答案】72；108
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：234引用：3難度：0.2
相似題
-
1．觀察猜想
（1）如圖1，在等邊△ABC與等邊△ADE中，△ADE繞點(diǎn)A順時(shí)針旋轉(zhuǎn)α度（0＜α＜360），則線段BD與線段CE的數(shù)量關(guān)系是 ，直線BD與直線CE相交所成較小角的度數(shù)是 ；
類比探究
（2）如圖2，在△ABC與△ADE中，∠BCA=∠DEA=90°，CB=CA，ED=EA，其他條件不變，（1）中的兩個(gè)結(jié)論是否成立？若成立，請(qǐng)說(shuō)明理由；若不成立，請(qǐng)寫出新的結(jié)論并證明；
拓展應(yīng)用
（3）如圖3，在△ABC與△ADE中，∠ABC=∠ADE=90°，∠BAC=∠DAE=60°，AB=3AD=3，當(dāng)B，D，E三點(diǎn)共線時(shí)，直接寫出CE的值．3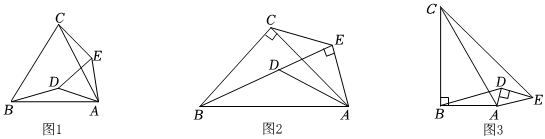
發(fā)布：2025/5/24 20:0:2組卷：208引用：1難度：0.1 -
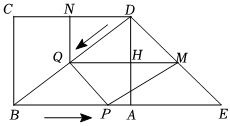2．已知：如圖，在矩形ABCD和等腰Rt△ADE中，AB=8cm,AD=AE=6cm,∠DAE=90°．點(diǎn)P從點(diǎn)B出發(fā)，沿BA方向勻速運(yùn)動(dòng)．速度為1cm/s；同時(shí)，點(diǎn)Q從點(diǎn)D出發(fā)，沿DB方向勻速運(yùn)動(dòng)，速度為1cm/s.過(guò)點(diǎn)Q作QM∥BE，交AD于點(diǎn)H，交DE于點(diǎn)M，過(guò)點(diǎn)Q作QN∥BC，交CD于點(diǎn)N．分別連接PQ，PM，設(shè)運(yùn)動(dòng)時(shí)間為t（s）（0＜t＜8）．
解答下列各題：
（1）當(dāng)PQ⊥BD時(shí)，求t的值；
（2）設(shè)五邊形PMDNQ的面積為S（cm2），求S與t之間的函數(shù)關(guān)系式．發(fā)布：2025/5/24 22:0:1組卷：27引用：1難度：0.4 -
3．如圖1，△ABC中，∠ABC=45°，AH⊥BC于點(diǎn)H，點(diǎn)D在AH上，且DH=CH，連結(jié)BD．
（1）求證：BD=AC；
（2）將△BHD繞點(diǎn)H旋轉(zhuǎn)，得到△EHF（點(diǎn)B，D分別與點(diǎn)E，F(xiàn)對(duì)應(yīng)），連接AE．
①如圖2，當(dāng)點(diǎn)F落在AC上時(shí)（F不與C重合），若CF=1，tanC=3，求AE的長(zhǎng)；
②如圖3，當(dāng)△EHF是由△BHD繞點(diǎn)H逆時(shí)針旋轉(zhuǎn)30°得到時(shí)，設(shè)射線CF與AE相交于點(diǎn)G，連接GH，試探究線段GH與EF之間滿足的數(shù)量關(guān)系，并說(shuō)明理由．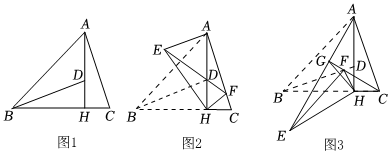
發(fā)布：2025/5/24 20:30:2組卷：60引用：1難度：0.1