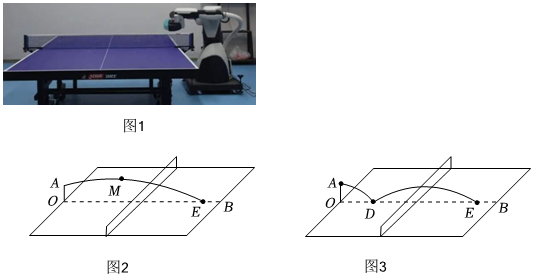
圖1是張帶智能發(fā)球機的乒乓球桌，它可以自定義設置球的落點、速度、弧度及旋轉方式，能更真實地模擬實戰(zhàn)．圖2是發(fā)球機從中線OB的端點O的正上方0.3m處的A點發(fā)球，球呈拋物線在OB正上方飛行，當飛行的水平距離為1m時，達到最高點M，其高度為0.4m.以O為原點，OB，OA所在直線分別為x軸，y軸建立平面直角坐標系．
（1）求圖2中拋物線的表達式．
（2）記圖2中的落球點為點E，則OE的長為多少？
（3）圖3是為了更好地模擬與人對打，將出球方向改變，調整成兩跳球的方式，即球從點A落到點D，再反彈過網落下，反彈后球呈拋物線飛行，且形狀與圖2中的拋物線形狀保持不變，但反彈后的最高高度變?yōu)?.2m.若最后球也落在點E，則OD的長為多少？
【考點】二次函數(shù)綜合題．
【答案】（1）y=-0.1（x-1）2+0.4；
（2）OE=3m；
（3）OD長為（3-2）m．
（2）OE=3m；
（3）OD長為（3-2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/10/11 22:0:1組卷：376引用：5難度：0.4
相似題
-
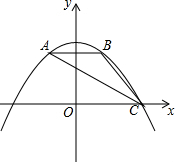1．如圖，拋物線y=ax2+經過△ABC的三個頂點，點A坐標為（-1，2），點B是點A關于y軸的對稱點，點C在x軸的正半軸上．94
（1）求該拋物線的函數(shù)關系表達式；
（2）點F為線段AC上一動點，過F作FE⊥x軸，F(xiàn)G⊥y軸，垂足分別為E、G，當四邊形OEFG為正方形時，求出F點的坐標．發(fā)布：2025/6/16 19:30:1組卷：730引用：9難度：0.4 -
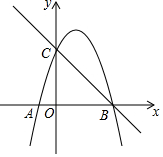2．如圖，直線y1=-x+3與x軸于交于點B，與y軸交于點C．拋物線y2=-x2+bx+c經過B、C兩點，并與x軸另一個交點為A．
（1）求拋物線y2的解析式；
（2）若點M在拋物線上，且S△MOC=4S△AOC，求點M的坐標；
（3）設點P是線段BC上一動點，過P作PQ⊥x軸，交拋物線于點Q，求線段PQ長度的最大值．發(fā)布：2025/6/17 2:0:1組卷：1010引用：3難度：0.3 -
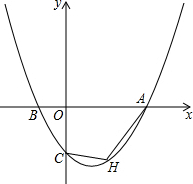3．如圖，已知拋物線y=ax2+bx+c過點A（6，0），B（-2，0），C（0，-3）．
（1）求此拋物線的解析式；
（2）若點H是該拋物線第四象限的任意一點，求四邊形OCHA的最大面積；
（3）若點Q在x軸上，點G為該拋物線的頂點，且∠QGA=45°，求點Q的坐標．發(fā)布：2025/6/16 23:0:1組卷：401引用：5難度：0.5