【問題背景】17世紀有著“業余數學家之王”美譽的法國律師皮耶?德?費馬，提出一個問題：求作三角形內的一個點，使它到三角形三個頂點的距離之和最小后來這點被稱之為“費馬點”．如圖1，點P是△ABC內的一點，將△APC繞點A逆時針旋轉60°到△AP'C'，則可以構造出等邊△APP'，得AP=PP'，CP=CP'，所以PA+PB+PC的值轉化為PP'+PB+P'C'的值，當B，P，P'，C四點共線時，線段BC′的長為所求的最小值，即點P為△ABC的“費馬點”．
【拓展應用】
（1）如圖2，點P是等邊△ABC內的一點，連接PA，PB，PC，將△PAC繞點A逆時針旋轉60°得到△AP'C'．
①若PA=3，則點P與點P'之間的距離是 33；
②當PA=3，PB=4，PC=5時，求∠AP′C′的大小；
（2）如圖3，點P是△ABC內的一點，且∠BAC=90°，AB=6，AC=23，求PA+PB+PC的最小值．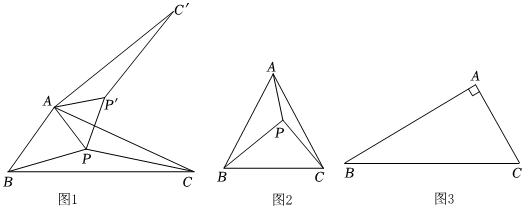
AC
=
2
3
【考點】幾何變換綜合題．
【答案】3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：454引用：1難度：0.4
相似題
-
1．如圖1～圖3所示，△ABC是直角三角形，∠BCA=90°，AC＞BC．點O是射線AC上的一點，點M是射線BC上的一點，且BM=OA，把點M繞點O逆時針旋轉90°落在點N處，直線AN和直線OB相交于點P．
（1）當點O與點C重合時，點N必然落在AC上，且點P與點C重合，如圖2所示，請你直接寫出此時線段AN與線段OB的數量關系及∠APB的大小；
（2）當點O在如圖1所示的位置時，（1）中關于線段AN和線段OB的數量關系及∠APB大小的結論還成立嗎？如果成立，請給出證明過程；如果不成立，請說明理由；
（3）當點O在如圖3所示的位置時，（1）中關于線段AN和線段OB的數量關系及∠APB大小的結論還成立嗎？請直接給出結論，不用說明理由.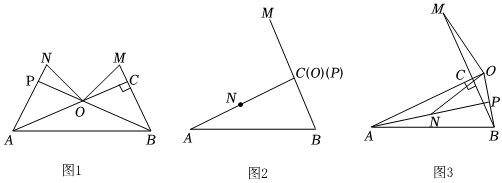
發布：2025/6/8 15:30:1組卷：36引用：1難度：0.2 -
2．（1）感知：如圖①，在Rt△ABC中，∠ACB=90°．D，E分別是AC，BC的中點，連結DE．則△CDE和△CAB的面積比是 ．
（2）探究：將圖①中△CDE繞點C順時針旋轉，使點E在△CAB的內部．再連結AD，EF，延長BE交AC于點O，交AD于點F，如圖②．
①求證：△ACD～△BCE；②求證：AD⊥BF；
（3）拓展：將圖①中的△CDE繞點C順時針旋轉90°，使點D恰好落在BC的延長線上，點E在AC上．連結AD，BE，并延長BE交AD與點F，其他條件不變，如圖③．若AC=8，BC=6，求BF的長．
發布：2025/6/8 15:30:1組卷：15引用：1難度：0.4 -
3．已知△ABC，∠ACB=90°，AC=BC．
（1）如圖1，將邊AB繞點B順時針旋轉至BP的位置，BP交AC于點Q，連接CP，使得CP∥AB．若BC=2，求CP的長度；2
（2）如圖2，點G在AC邊上，將線段CG繞點C順時針旋轉90°得到線段CE，連接EG并延長交AB于點H，D是線段HB上一點，AH=DH，連接ED，CH．求證：ED=CH；2
（3）如圖3，延長BA至點P，使PA=AB，連接PC，將線段PC繞點C順時針旋轉90°得到線段CT，連接AT，過點C作CK⊥AB于點K，點G在線段AK上，連接TG，將△TAG沿TG翻折，點A的對應點A'恰好落在CK上，M是邊BC上一點，連接GM，將△BGM沿GM翻折到△B'GM，B'G與BC交于點H．當點G，A'，B'共線時，直接寫出12的值．HMMB′
發布：2025/6/8 20:30:2組卷：348引用：1難度：0.1