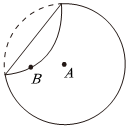
折紙是一種以紙張折成各種不同形狀的藝術活動，折紙大約起源于公元1世紀或者2世紀時的中國，折紙與自然科學結合在一起，不僅成為建筑學院的教具，還發展出了折紙幾何學成為現代幾何學的一個分支．如圖，現有一半徑為4的圓紙片（A為圓心，B為圓內的一定點），且|AB|=2，如圖將圓折起一角，使圓周正好過點B，把紙片展開，并留下一條折痕，折痕上到A，B兩點距離之和最小的點為P，如此往復，就能得到越來越多的折痕，設P點的軌跡為曲線C．在C上任取一點M，則△MAB面積的最大值是（　　）

A．2

B．3

C．

D．

【考點】軌跡方程．

【答案】D

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/4/20 14:35:0組卷：33引用：6難度：0.5

相似題

1．點P為△ABC所在平面內的動點，滿足
AP
=t（
AB
|
AB
|
cos
B
+
AC
|
AC
|
cos
C
），t∈（0，+∞），則點P的軌跡通過△ABC的（　　）
A．外心 B．重心 C．垂心 D．內心
發布：2024/12/29 6:30:1組卷：106引用：3難度：0.7
解析
2．已知四棱錐P-ABCD的底面ABCD為正方形，PD⊥底面ABCD，且PD=AD=4，點E為BC的中點．四棱錐P-ABCD的所有頂點都在同一個球面上，點M是該球面上的一動點，且PM⊥AE，則點M的軌跡的長度為（　　）
A．6π B．
32
π
5
C．
2
70
π
5
D．
4
70
π
5
發布：2024/12/29 8:0:12組卷：14引用：1難度：0.6
解析
3．已知兩個定點A（-2，0），B（1，0），如果動點P滿足|PA|=2|PB|．
（1）求點P的軌跡方程并說明該軌跡是什么圖形；
（2）若直線l：y=kx+1分別與點P的軌跡和圓（x+2）²+（y-4）²=4都有公共點，求實數k的取值范圍．
發布：2024/12/29 10:30:1組卷：42引用：3難度：0.5
解析

相關試卷

1．點P為△ABC所在平面內的動點，滿足AP=t（AB|AB|cosB+AC|AC|cosC），t∈（0，+∞），則點P的軌跡通過△ABC的（ ）