2023年山西省省際名校聯考高考數學二模試卷（A）

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．復數z滿足（1-i）²z=1+i,則|z|=（　　）

  A． 2 2

  B． 1 2

  C． 2

  D．2
  組卷：59引用：3難度：0.8

  解析

• 2．設A是一個數集，且至少含有兩個數，若對任意a,b∈A，都有

  a

  +

  b

  ,

  a

  -

  b

  ,

  ab

  ,

  a

  b

  ∈

  A

  （除數b≠0），則稱A是一個數域，則下列集合為數域的是（　　）

  A．N

  B．Z

  C．Q

  D．{x|x≠0，x∈R}
  組卷：126引用：3難度：0.7

  解析

• 3．如圖，在△ABC中，D是BC邊中點，

  AP

  =

  1

  3

  AD

  ，CP的延長線與AB交于AN，則（　　）

  A． AN = 1 4 AB

  B． AN = 1 5 AB

  C． AN = 1 6 AB

  D． AN = 1 7 AB
  組卷：74引用：3難度：0.8

  解析

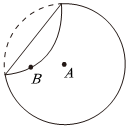• 4．折紙是一種以紙張折成各種不同形狀的藝術活動，折紙大約起源于公元1世紀或者2世紀時的中國，折紙與自然科學結合在一起，不僅成為建筑學院的教具，還發展出了折紙幾何學成為現代幾何學的一個分支．如圖，現有一半徑為4的圓紙片（A為圓心，B為圓內的一定點），且|AB|=2，如圖將圓折起一角，使圓周正好過點B，把紙片展開，并留下一條折痕，折痕上到A，B兩點距離之和最小的點為P，如此往復，就能得到越來越多的折痕，設P點的軌跡為曲線C．在C上任取一點M，則△MAB面積的最大值是（　　）

  A．2

  B．3

  C． 2

  D． 3
  組卷：33引用：6難度：0.5

  解析

• 5．小李，小王相約周日到晉祠游玩，兩人約定早上7：00各自從家出發，小李乘坐301路公交，路上所需時間（單位：分鐘）服從正態分布N（44，4）．小王乘坐804路公交，路上所需時間（單位：分鐘）服從正態分布N（40，16）．下列說法從統計角度可認為不合理的是（　　）
  參考數據：Z～N（μ，σ²），則P（μ-σ＜Z＜μ+σ）=0.682，P（μ-2σ＜Z＜μ+2σ）=0.9545，P（μ-3σ＜Z＜μ+3σ）≈0.9973）

  A．小王在7：28前到達晉祠的可能性不超過1%

  B．小王比小李在7：50前到達晉桐的可能性更小

  C．小李和小王在7：48前到達晉祠的可能性一樣

  D．小李比小王在7：44前到達晉祠的可能性更大
  組卷：84引用：3難度：0.6

  解析

• 6．已知a≤1，函數f（x）=（x-1）e^x-

  a

  3

  x

  3

  -

  1

  2

  x

  2

  （

  x

  ≥

  0

  ）

  ，則（　　）

  A．f（x）有最小值，有最大值

  B．f（x）無最小值，有最大值

  C．f（x）有最小值，無最大值

  D．f（x）無最小值，無最大值
  組卷：43引用：3難度：0.7

  解析

• 7．正四棱柱ABCD-A₁B₁C₁D₁中，AB=2，P為上底面A₁B₁C₁D₁的中心，M是棱AB的中點，正四棱柱的高

  h

  ∈

  [

  3

  ，

  2

  2

  ]

  ，點M到平面PCD的距離的取值范圍是（　　）

  A． [ 3 ， 32 9 ]

  B． [ 3 ， 4 2 3 ]

  C． [ 3 ， 2 ]

  D． [ 1 4 ， 1 3 ]
  組卷：65引用：4難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知雙曲線E：

  x

  2

  3

  -

  y

  2

  =

  1

  的左、右焦點分別為F₁，F₂，A是直線l：

  y

  =

  -

  2

  3

  x

  上不同于原點O的一個動點，斜率為k₁的直線AF₁與雙曲線E交于M，N兩點，斜率為k₂的直線AF₂與雙曲線E交于P，Q兩點．
  （1）求

  1

  k

  1

  +

  1

  k

  2

  的值；
  （2）若直線OM，ON，OP，OQ的斜率分別為k_OM，k_ON，k_OP，k_OQ，問是否存在點A，滿足k_OM+k_ON+k_OP+k_OQ=0，若存在，求出A點坐標；若不存在，說明理由．
  組卷：73引用：4難度：0.3

  解析

• 22．設函數f（x）=xsinx,x∈R．
  （1）求f（x）在區間（2kπ，2kπ+π），k∈N上的極值點個數；
  （2）若x₀為f（x）的極值點，則

  |

  f

  （

  x

  0

  ）

  |

  ＞

  λln

  （

  1

  +

  x

  2

  0

  ）

  ，求整數λ的最大值．
  組卷：36引用：3難度：0.2

  解析