探索：小明在研究數(shù)學(xué)問(wèn)題：已知AB∥CD，AB和CD都不經(jīng)過(guò)點(diǎn)P，探索∠P與∠C的數(shù)量關(guān)系．
發(fā)現(xiàn)：在圖1中，：∠APC=∠A+∠C；如圖5
小明是這樣證明的：過(guò)點(diǎn)P作PQ∥AB
∴∠APQ=∠A（ 兩直線平行，內(nèi)錯(cuò)角相等兩直線平行，內(nèi)錯(cuò)角相等）
∵PQ∥AB，AB∥CD．
∴PQ∥CD（ 平行于同一直線的兩直線平行平行于同一直線的兩直線平行）
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
（1）為小明的證明填上推理的依據(jù)；
（2）應(yīng)用：①在圖2中，∠P與∠A、∠C的數(shù)量關(guān)系為 ∠APC+∠A+∠C=360°∠APC+∠A+∠C=360°；
②在圖3中，若∠A=30°，∠C=70°，則∠P的度數(shù)為 40°40°；
（3）拓展：在圖4中，探究∠P與∠A，∠C的數(shù)量關(guān)系，并說(shuō)明理由．
【考點(diǎn)】平行線的判定與性質(zhì)．
【答案】兩直線平行，內(nèi)錯(cuò)角相等；平行于同一直線的兩直線平行；∠APC+∠A+∠C=360°；40°
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：445引用：5難度：0.3
相似題
-
1．推理填空
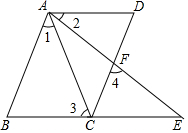
已知：如圖所示，點(diǎn)B，C，E在同一條直線上，AB∥CD，∠1=∠2，∠3=∠4，求證：AD∥BE
證明：∵AB∥CD（已知）
∴∠4=∠（）
∵∠3=∠4（已知）∴∠3=∠（）
∴∠1=∠2（已知）∴∠1+∠CAF=∠2+∠CAF（等式的性質(zhì)）
即∠BAF=∠DAC
∴∠3=∠（等量代換）
∴AD∥BE（）發(fā)布：2025/6/16 0:30:2組卷：540引用：3難度：0.8 -
2．如圖，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列結(jié)論：
①BC平分∠ABE；
②AC∥BE；
③∠CBE+∠EDB=90°；
④∠DEB=2∠ABC，其中正確的有（ ）發(fā)布：2025/6/15 23:0:1組卷：1639引用：9難度：0.5 -
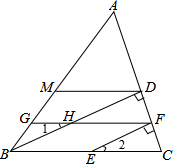3．已知BD⊥AC于點(diǎn)D，EF⊥AC于點(diǎn)F，∠AMD=∠AGF，∠1=∠2=28°．
（1）求∠GFC的度數(shù)；
（2）求證：DM∥BC．發(fā)布：2025/6/15 23:0:1組卷：482引用：4難度：0.6