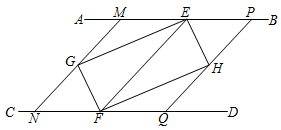
如圖，AB∥CD，點E，F分別在AB，CD上，連接EF，∠AEF、∠CFE的平分線交于點G，∠BEF、∠DFE的平分線交于點H．
（1）求證：四邊形EGFH是矩形；
（2）小明在完成（1）的證明后繼續進行了探索，過G作MN∥EF，分別交AB，CD于點M，N，過H作PQ∥EF，分別交AB，CD于點P，Q，得到四邊形MNQP，此時，他猜想四邊形MNQP是菱形，請在框中補全他的證明思路．
| 由AB∥CD，MN∥EF，PQ∥EF，易證四邊形MNQP是平行四邊形，要證?MNQP是菱形，只要證 MN=NQ，已知條件 FG平分∠CFE FG平分∠CFE ，MN∥EF，故只要證GM=FQ，即證△MGE≌△QFH，易證GE=FH GE=FH 、∠GME=∠FQH ∠GME=∠FQH .故只要證∠MGE=∠QFH，易證∠MGE=∠GEF，∠QFH=∠EFH，∠GEF=∠EFH ∠GEF=∠EFH ，即可得證． |
【答案】FG平分∠CFE；GE=FH；∠GME=∠FQH；∠GEF=∠EFH
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：104引用：5難度：0.5
相似題
-
1．如圖，菱形ABCD的對角線AC，BD相交于點O，E是AD的中點，點F，G在AB上，EF⊥AB，OG∥EF．
（1）求證：四邊形OEFG是矩形；
（2）若AD=20，EF=8，求OE和BG的長．發布：2025/6/5 20:30:1組卷：897引用：11難度：0.6 -
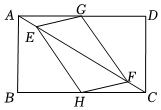2．在矩形ABCD中，AB=6，BC=8，E、F是對角線AC上的兩個動點，分別從A、C同時出發相向而行，速度均為每秒1個單位長度，運動時間為t秒，其中0≤t≤10．
（1）若G，H分別是AD，BC中點，則四邊形EGFH一定是怎樣的四邊形（E、F相遇時除外）？
答：；（直接填空，不用說理）
（2）在（1）條件下，若四邊形EGFH為矩形，求t的值；
（3）在（1）條件下，若G向D點運動，H向B點運動，且與點E，F以相同的速度同時出發，若四邊形EGFH為菱形，求t的值．發布：2025/6/6 0:0:1組卷：4824引用：26難度：0.4 -
3．如圖，在?ABCD中，AC⊥CD．
（1）延長DC到E，使CE=CD，連接BE，求證：四邊形ABEC是矩形；
（2）若點F，G分別是BC，AD的中點，連接AF，CG，試判斷四邊形AFCG是什么特殊的四邊形？并證明你的結論．發布：2025/6/6 0:0:1組卷：1065引用：4難度：0.5