某裝置用電場控制帶電粒子運動，工作原理如圖所示．矩形ABCD區域內存在多層緊鄰的勻強電場，每層的高度均為d,電場強度大小均為E，方向沿豎直方向交替變化．AB邊長為12d,BC邊長為8d.質量為m、電荷量為+q的粒子流從裝置左端中點射入電場，粒子初動能為Ek，入射角為θ，在紙面內運動．不計重力及粒子間的相互作用力。
（1）當θ=θ0時，若粒子能從CD邊射出，求該粒子通過電場的時間t。
（2）當Ek=4qEd時，若粒子從CD邊射出電場時與軸線OO'的距離小于d,求入射角θ的范圍。
（3）當Ek=83qEd,粒子在θ為-π2～π2范圍內均勻射入電場，求從CD邊出射的粒子與入射粒子的數量之比N：N0。
8
3
π
2
～
π
2
【考點】從能量轉化與守恒的角度解決電場中的問題．
【答案】（1）當θ=θ0時，若粒子能從CD邊射出，該粒子通過電場的時間為；
（2）當Ek=4qEd時，若粒子從CD邊射出電場時與軸線OO'的距離小于d，則入射角θ的范圍為-30°＜θ＜30°；
（3）當Ek=qEd，粒子在θ為-范圍內均勻射入電場，求從CD邊出射的粒子與入射粒子的數量之比為50%
8
d
cos
θ
0
?
m
2
E
k
（2）當Ek=4qEd時，若粒子從CD邊射出電場時與軸線OO'的距離小于d，則入射角θ的范圍為-30°＜θ＜30°；
（3）當Ek=
8
3
π
2
～
π
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1342引用：3難度：0.2
相似題
-
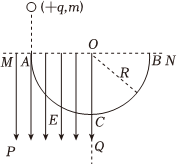1．如圖所示，ABC為光滑的固定在豎直面內的半圓形軌道，軌道半徑為R=0.4m,A、B為半圓軌道水平直徑的兩個端點，O為圓心．在水平線MN以下和豎直線OQ以左的空間內存在豎直向下的勻強電場，電場強度E=1.0×106N/C．現有一個質量m=2.0×10-2kg,電荷量q=2.0×10-7C的帶正電小球（可看作質點），從A點正上方由靜止釋放，經時間t=0.3s到達A點并沿切線進入半圓軌道，g=10m/s2，不計空氣阻力及一切能量損失，求：
（1）小球經過C點時對軌道的壓力大小；
（2）小球經過B點后能上升的最大高度．發布：2024/12/29 20:0:1組卷：750引用：4難度：0.5 -
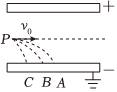2．11H、12H、13H三個原子核，電荷均為e,質量之比為1：2：3，如圖所示，它們以相同的初速度由P點平行極板射入勻強電場，在下極板的落點為A、B、C，已知上極板帶正電，原子核不計重力，下列說法正確的是（ ）發布：2024/12/29 21:30:1組卷：374引用：5難度：0.6 -
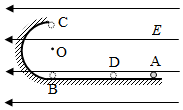3．如圖，在豎直平面內，一半徑為R的半圓形軌道與水平軌道在B點平滑連接．半圓形軌道的最低點為B、最點高為C，圓心為O．整個裝置處水平向左的勻強電場中．現讓一質量為m、電荷量為q的帶正電小球（可視為質點），從水平軌道的A點靜止釋放，到達B點時速度為．當小球過C點時撤去電場，小球落到水平軌道上的D點．已知A、B間的距離為5gRR，重力加速度為g,軌道絕緣且不計摩擦和空氣阻力，求：103
（1）該勻強電場場強E的大小；
（2）A、D間的距離；
（3）小球經過半圓形軌道某點P（圖中未畫出）時，所受合外力方向指向圓心O，求小球過P點時對軌道壓力的大小．發布：2024/12/29 20:30:1組卷：59引用：2難度：0.7
相關試卷