【閱讀理解】
我們知道,1+2+3+…+n=n(n+1)2,那么12+22+32+…+n2結果等于多少呢?
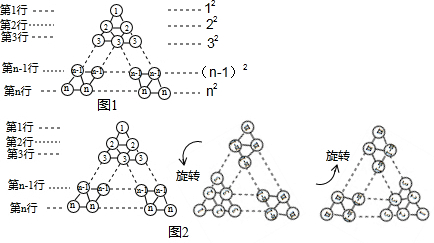
在圖1所示三角形數陣中,第1行圓圈中的數為1,即12,第2行兩個圓圈中數的和為2+2,即22,…;第n行n個圓圈中數的和為n個nn+n+…+n,即n2,這樣,該三角形數陣中共有n(n+1)2個圓圈,所有圓圈中數的和為12+22+32+…+n2.
【規律探究】
將三角形數陣經兩次旋轉可得如圖2所示的三角形數陣,觀察這三個三角形數陣各行同一位置圓圈中的數(如第n-1行的第一個圓圈中的數分別為n-1,2,n),發現每個位置上三個圓圈中數的和均為 2n+12n+1,由此可得,這三個三角形數陣所有圓圈中數的總和為:3(12+22+32+…+n2)=n(n+1)(2n+1)2n(n+1)(2n+1)2,因此,12+22+32+…+n2=n(n+1)(2n+1)6n(n+1)(2n+1)6.
【解決問題】
根據以上發現,計算:12+22+32+…+201721+2+3+…+2017的結果為 13451345.
n
(
n
+
1
)
2
n
個
n
n
+
n
+
…
+
n
n
(
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
6
n
(
n
+
1
)
(
2
n
+
1
)
6
1
2
+
2
2
+
3
2
+
…
+
201
7
2
1
+
2
+
3
+
…
+
2017
【考點】規律型:數字的變化類.
【答案】2n+1;;;1345
n
(
n
+
1
)
(
2
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
6
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/16 20:0:8組卷:2167引用:15難度:0.6
相似題
-
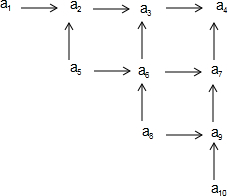 1.把10個兩兩互不相等的正整數a1,a2,…,a10寫成圖表的形式,其中兩個箭頭所指的數等于這兩個箭頭始點兩個數之和(如a2=a1+a5),則a4的最小可能值是.發布:2025/5/29 8:30:1組卷:70引用:1難度:0.7
1.把10個兩兩互不相等的正整數a1,a2,…,a10寫成圖表的形式,其中兩個箭頭所指的數等于這兩個箭頭始點兩個數之和(如a2=a1+a5),則a4的最小可能值是.發布:2025/5/29 8:30:1組卷:70引用:1難度:0.7 -
2.觀察下列數據,按某種規律在橫線上填上適當的數:
,,.1,-34,59,-716發布:2025/5/29 8:30:1組卷:164引用:13難度:0.9 -
3.將正偶數按右表排列成5列:根據表中的規律,偶數2004應排在第 行,第 列.
第1列 第2列 第3列 第4列 第5列 第一行 2 4 6 8 第二行 16 14 12 10 第三行 18 20 22 24 第四行 32 30 28 26 … … … … … 發布:2025/5/29 8:0:2組卷:50引用:1難度:0.5


