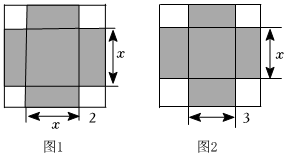
《代數(shù)學(xué)》中記載，形如x2+8x=33的方程，求正數(shù)解的幾何方法是：“如圖1，先構(gòu)造一個(gè)面積為x2的正方形，再以正方形的邊長(zhǎng)為一邊向外構(gòu)造四個(gè)面積為2x的矩形，陰影部分的面積 為33，得到大正方形的面積為33+16=49，所以（x+2+2）2=49，則該方程的正數(shù)解為7-4=3．”小聰按此方法解關(guān)于x的方程x2+12x=m時(shí)，構(gòu)造出如圖2所示的圖形，已知陰影部分的面積為64．則該方程的正數(shù)解為x=44．
【考點(diǎn)】一元二次方程的應(yīng)用；解一元二次方程-直接開(kāi)平方法．
【答案】4
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/23 12:30:2組卷：78引用：3難度：0.5
相似題
-
1．隨著人們經(jīng)濟(jì)收入的不斷提高及汽車產(chǎn)業(yè)的快速發(fā)展，普通家庭擁有汽車的夢(mèng)想已經(jīng)實(shí)現(xiàn)，私家車出行居民消費(fèi)的時(shí)尚．據(jù)某市交通部門(mén)統(tǒng)計(jì)，2020年底全市汽車擁有量為192萬(wàn)輛，而截止到2022年底，全市的汽車擁有量已達(dá)300萬(wàn)輛．
（1）求2020年底至2022年底該市汽車擁有量的年平均增長(zhǎng)率；
（2）為保護(hù)城市環(huán)境，緩解汽車擁堵?tīng)顩r，該市交通部門(mén)擬控制汽車總量，要求到2024年底全市汽車擁有量不超過(guò)336.1萬(wàn)輛；另?yè)?jù)估計(jì)，從2023年初起，該市此后每年報(bào)廢的汽車數(shù)量是上年底汽車擁有量的10%．假定每年新增汽車數(shù)量相同，請(qǐng)你計(jì)算出該市每年新增汽車數(shù)量最多不能超過(guò)多少萬(wàn)輛．發(fā)布：2025/5/23 22:0:2組卷：50引用：1難度：0.5 -
2．有一人患了流感，經(jīng)過(guò)兩輪傳染后共有64人患了流感，那么每輪傳染中平均一個(gè)人傳染給個(gè)人．
發(fā)布：2025/5/24 2:30:1組卷：2099引用：25難度：0.7 -
3．疫情期間居民為了減少外出時(shí)間，更愿意使用APP在線上買(mǎi)菜，某買(mǎi)菜APP今年一月份新注冊(cè)用戶為200萬(wàn)，三月份新注冊(cè)用戶為338萬(wàn)，則二、三兩個(gè)月新注冊(cè)用戶每月平均增長(zhǎng)率是（ ）
發(fā)布：2025/5/24 3:0:1組卷：822引用：8難度：0.6