如圖，在△ABC中，∠ACB=90°，CA=CB=4，點D在BC上，且BD=2，以B為圓心，將BD順時針旋轉180°形成半圓?DBF，P為半圓上任意一點，線段CP繞著點C順時針旋轉90°，得到線段CE，連接PB，AE．
（1）求證：AE=BP；
（2）若CP與半圓相切，求CP的長度；
（3）當S△BCP=2時，求∠CBP的度數以及此時扇形DBP的面積．
?
DBF
【考點】圓的綜合題．
【答案】（1）見解析；（2）；（3）∠CBP=30°，扇形DBP的面積是．
2
3
π
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：255引用：3難度：0.4
相似題
-
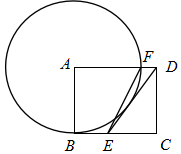1．如圖，在矩形ABCD中，點E是BC邊上一點，且AD=DE，以AB為半徑作⊙A，交AD邊于點F，連接EF．
（1）求證：DE是⊙A的切線；
（2）若AB=2，BE=1，求AD的長；
（3）在（2）的條件下，求tan∠FED．發布：2025/5/24 17:30:1組卷：161引用：2難度：0.4 -
2．（1）如圖1，⊙A的半徑為2，AB=5，點P為⊙A上任意一點，則BP的最小值為 ．
（2）如圖2，已知矩形ABCD，點E為AB上方一點，連接AE，BE，作EF⊥AB于點F，點P是△BEF的內心，求∠BPE的度數．
（3）如圖3，在（2）的條件下，連接AP，CP，若矩形的邊長AB=6，BC=4，BE=BA，求此時CP的最小值．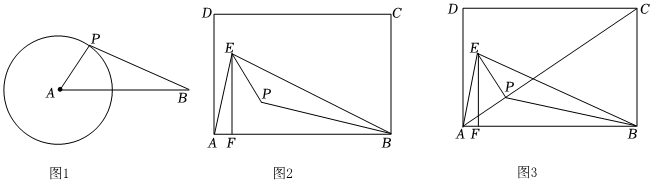
發布：2025/5/24 16:30:1組卷：1241引用：6難度：0.3 -
3．微探究：如圖①，點P在⊙O上，利用直尺（沒有刻度）和圓規過點P作⊙O的切線．小明所在的數學小組經過合作探究，發現了很多作法，精彩紛呈．
作法一：
①作直徑PA的垂直平分線交⊙O于點B；
②分別以點B、P為圓心，OP為半徑作弧，兩弧交于點C；
③作直線PC．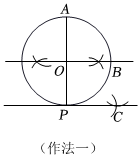
作法二：
①作直徑PA的四等分點B、C；
②以點A為圓心，CA為半徑作弧，交射線PA于點D；
③分別以點A、P為圓心，PD、PC為半徑作弧，兩弧交于點E；
④作直線PE．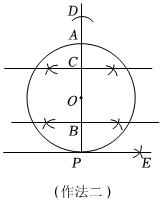
（1）以上作法是否正確？選一個你認為正確的作法予以證明；
（2）在圖①、圖②中用兩種作法作出符合條件的圖形（與以上作法不同）．不寫作法，保留作圖痕跡．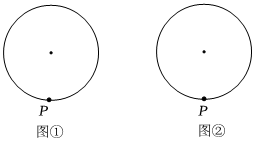
發布：2025/5/24 16:0:1組卷：115引用：1難度：0.1