材料：如何將雙重二次根式a±2b（a＞0，b＞0，a±2b＞0）化簡呢？如能找到兩個數m,n（m＞0，n＞0），使得（m）2+（n）2=a,即m+n=a,且使m?n=b，即m?n=b,那么a±2b=（m）2+（n）2±2m?n=（m±n）2∴a±2b=|m±n|，雙重二次根式得以化簡．
例如化簡：3±22因為3=1+2且2=1×2∴3±22=（1）2+（2）2±21×2∴3±22=|1±2|．
由此對于任意一個二次根式只要可以將其化成a±2b的形式，且能找到m,n（m＞0，n＞0）使得m+n=a,且m?n=b,那么這個雙重二次根式一定可以化簡為一個二次根式．
請同學們通過閱讀上述材料，完成下列問題：
（1）填空：5±26=3±23±2，12±235=7±57±5；
（2）化簡：9±62；
（3）計算：3-5+2±3．
a
±
2
b
b
m
n
m
?
n
b
a
±
2
b
m
n
m
?
n
m
n
a
±
2
b
|
m
±
n
|
3
±
2
2
2
1
2
1
2
∴
3
±
2
2
2
a
±
2
b
5
±
2
6
3
2
3
2
12
±
2
35
7
5
7
5
9
±
6
2
3
-
5
2
±
3
【考點】二次根式的性質與化簡．
【答案】±；±
3
2
7
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 6:30:2組卷：1675引用：2難度：0.5
相似題
-
1．閱讀材料：
小明在學習二次根式后，發現一些含根號的式子可以寫成另一個式子的平方，如3+2=（1+2）2．善于思考的小明進行了以下探索：2
設a+b=（m+n2）2（其中a、b、m、n均為整數），則有a+b2=m2+2n2+2mn2．2
∴a=m2+2n2，b=2mn.
這樣小明就找到了一種把類似a+b的式子化為平方式的方法．2
請你仿照小明的方法探索并解決下列問題：
（1）當a、b、m、n均為正整數時，若a+b=（m+n3）2，用含m、n的式子分別表示a、b,得：a=，b=；3
（2）利用所探索的結論，找一組正整數a、b、m、n,填空：+=（ +3）2；3
（3）若a+4=（m+n3）2，且a、m、n均為正整數，求a的值？3
（4）化簡：．6+25發布：2025/6/4 22:0:2組卷：578引用：1難度：0.5 -
2．若m是正整數，m除以13的余數為2，則稱m是“阿二數”．例如：15是正整數，15÷13=1?2，則15是“阿二數”；52是正整數，且52÷13=4，則52不是“阿二數”，對于任意四位正整數p,p的千位數字為a,百位數字為b,十位數字為c,個位數字為d.有一個四位正整數p是“阿二數”，p的千位數字比百位數字少1，十位數字與個位數字的和為9，且
為有理數，則滿足條件的p的值為 ．F（p）=5c+7d2a+b發布：2025/6/4 21:30:2組卷：152引用：1難度：0.6 -
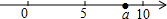3．實數a在數軸上的位置如圖所示，則+（2a-3）2化簡后為（a-15）2．發布：2025/6/4 20:30:1組卷：80引用：1難度：0.9