如圖，在平行四邊形ABCD中，點E是BC邊上的動點，已知AB=4，BC=6，現將△ABE沿AE折疊，點B′是點B的對應點，
（1）如圖1，當點B′恰好落在AD邊上時，求：CE的值．
（2）如圖2，若∠B=60°，點B′落在DE上時，求B′D（保留根號）．
（3）如圖2，若∠EAD=m∠BAD，∠EDA=（1-2m）∠CDA，當∠AED的值與∠CDA的度數無關時，求m的值并求出此時∠AED的度數．
【考點】四邊形綜合題．
【答案】（1）CE=2；
（2）；
（3）；∠AED=120°．
（2）
B
′
D
=
2
6
-
2
（3）
m
=
1
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：385引用：3難度：0.4
相似題
-
1．如圖1，正方形ABCD中，AC為對角線，點P在線段AC上運動，以DP為邊向右作正方形DPFE，連接CE；
【初步探究】
（1）則AP與CE的數量關系是 ，AP與CE的夾角度數為 ；
【探索發現】
（2）點P在線段AC及其延長線上運動時，如圖1，圖2，探究線段DC，PC和CE三者之間的數量關系，并說明理由；
【拓展延伸】
（3）點P在對角線AC的延長線上時，如圖3，連接AE，若AB=，AE=22，求四邊形DCPE的面積．213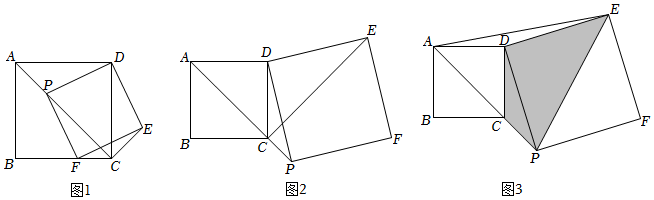
發布：2025/5/26 8:0:5組卷：2163引用：9難度：0.3 -
2．閱讀與思考
平移是初中幾何變換之一，它可以將線段和角平移到一個新的位置，從而把分散的條件集中到一起，使問題得以解決．平移包括以下三個方面的應用：一、分散的條件集中；二、復雜圖形變得簡單明了；三、轉化題目的形式．以下面例題來說明．
如圖1，在正方形中ABCD中，E，F，G分別是BC，CD，AD上的點，GE⊥BF于點O，那么GE=BF．
證明過程如下：
∵GE⊥BF于點O，
∴∠GOB=90°，
過點A作AH∥GE交BC于點H，交BF于點M．
∴∠AMB=∠GOB=90°，
∴∠ABM+∠BAM=90°，
∵四邊形ABCD為正方形，
∴AG∥HE，AB=BC，∠ABC=∠C=90°，
∴∠ABM+∠FBC=∠ABC=90°，
∴∠BAM=∠FBC，
∴△ABH≌△BCF（依據1），
∴AH=BF，
∵AH∥GE，AG∥HE，
∴四邊形AHEG為平行四邊形（依據2），
∴AH=GE，
∴GE=BF．
【閱讀理解】填空：上述閱讀材料中“依據1”是 ，“依據2”是 ．
【遷移嘗試】如圖2，在5×6的正方形網格中，點A，B，C，D為格點，AB交CD于點M．則∠AMC的度數為 ；
【拓展應用】如圖3，點P是線段AB上的動點，分別以AP，BP為邊在AB的同側作正方形APCD與正方形PBEF，連接DE分別交線段BC，PC于點M，N．求∠DMC的度數．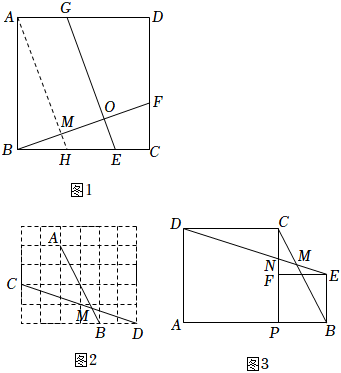
發布：2025/5/26 9:0:1組卷：217引用：2難度：0.3 -
3．在正方形ABCD中，對角線AC、BD相交于點O，F是正方形ABCD內一點，∠BFC=90°，將△BFC繞點C按順時針方向旋轉一定角度得到△DEC，點B、F的對應點分別為點D、E，則直線EF經過點O．
【方法感知】如圖①，當點F在△AOB內時，過點D作DG⊥DE交EF于點G，則∠DGE的大小為 度，DE、OE、OF的數量關系為 ．
【類比遷移】如圖②，當點F在△COD內時，試判斷DE、OE、OF之間的數量關系，并說明理由．
【拓展應用】如圖③，將正方形ABCD改為菱形，對角線AC、BD相交于點O，F是△COD內一點，∠BFC=90°．若將△BFC繞點C按順時針方向旋轉60°得到△DEC，點B、F的對應點分別為點D、E．若DE=2，則OE+OF=．2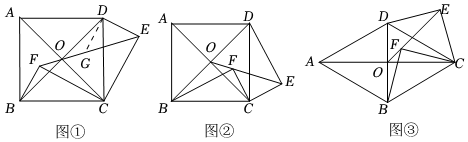
發布：2025/5/26 7:30:2組卷：160引用：1難度：0.3