《瀑布》（圖1）是最為人所知的作品之一，圖中的瀑布會源源不斷地落下，落下的水又逆流而上，荒唐至極，但又會讓你百看不膩，畫面下方還有一位饒有興致的觀察者，似乎他沒發現什么不對勁．此時，他既是畫外的觀看者，也是埃舍爾自己．畫面兩座高塔各有一個幾何體，左塔上方是著名的“三立方體合體”由三個正方體構成，右塔上的幾何體是首次出現，后稱“埃舍爾多面體”（圖2）
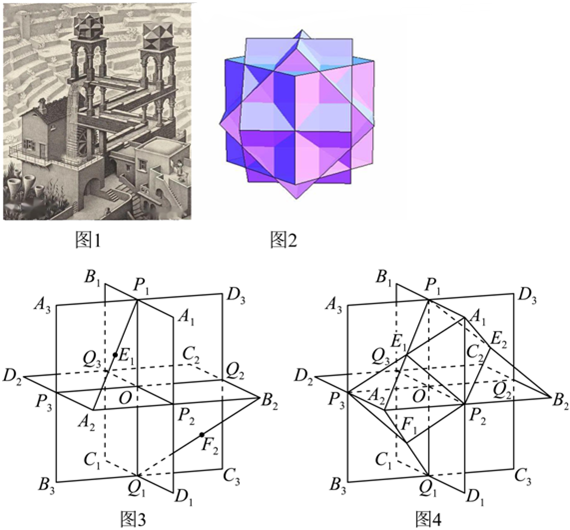
埃舍爾多面體可以用兩兩垂直且中心重合的三個正方形構造，設邊長均為2，定義正方形AnBnCnDn，n=1，2，3的頂點為“框架點”，定義兩正方形交線為“極軸”，其端點為“極點”，記為Pn，Qn，將極點P1，Q1，分別與正方形A2B2C2D2的頂點連線，取其中點記為Em，Fm，m=1，2，3，4，如（圖3）．埃舍爾多面體可視部分是由12個四棱錐構成，這些四棱錐頂點均為“框架點”，底面四邊形由兩個“極點”與兩個“中點”構成，為了便于理解，圖4我們構造了其中兩個四棱錐A1-P1E1P2E2與A2-P2E1P3F1
（1）求異面直線P1A2與Q1B2成角余弦值；
（2）求平面P1A1E1與平面A1E2P2的夾角正弦值；
（3）求埃舍爾體的表面積與體積（直接寫出答案）．
【考點】二面角的平面角及求法；棱柱、棱錐、棱臺的體積．
【答案】（1）；（2）；（3）表面積為，體積為2．
1
3
3
2
12
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：238引用：8難度：0.3
相似題
-
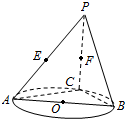1．如圖，AB是圓O的直徑，點C是圓O上異于A，B的點，直線PC⊥平面ABC，E，F分別是PA，PC的中點．
（Ⅰ）記平面BEF與平面ABC的交線為l,試判斷直線l與平面PAC的位置關系，并加以證明；
（Ⅱ）設（Ⅰ）中的直線l與圓O的另一個交點為D，且點Q滿足．記直線PQ與平面ABC所成的角為θ，異面直線PQ與EF所成的角為α，二面角E-l-C的大小為β．求證：sinθ=sinαsinβ．DQ=12CP發布：2025/1/20 8:0:1組卷：922引用：12難度：0.1 -
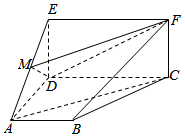2．如圖，四邊形ABCD為梯形，四邊形CDEF為矩形，平面ABCD⊥平面CDEF，∠BAD=∠ADC=90°，AB=AD=DE=CD，M為AE的中點．12
（1）證明：AC∥平面MDF；
（2）求平面MDF與平面BCF的夾角的大小．發布：2025/1/2 8:0:1組卷：141引用：1難度：0.6 -
3．如圖，AB是圓O的直徑，PA垂直于圓所在的平面，C是圓周上的點．
（1）求證：平面PAC⊥平面PBC；
（2）若AB=2，AC=2，PA=2，求二面角C-PB-A的度數．2發布：2025/1/28 8:0:2組卷：33引用：1難度：0.5