如圖，在△ABC中，AB=AC，以AB為直徑的⊙O與BC交于點(diǎn)D，連接AD．
（1）求證：BD=CD．
（2）若⊙O與AC相切，求∠B的度數(shù)．
（3）用無刻度的直尺和圓規(guī)作出劣弧?AD的中點(diǎn)E．（不寫作法，保留作圖痕跡）
?
AD
【考點(diǎn)】圓的綜合題．
【答案】（1）見解答過程；
（2）45°；
（3）見解答過程．
（2）45°；
（3）見解答過程．
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/22 16:30:1組卷：1387引用：8難度：0.6
相似題
-
1．【綜合與實(shí)踐】我國海域的島嶼資源相當(dāng)豐富，總面積達(dá)72800多平方公里，有人居住的島嶼達(dá)450個(gè)．位于北部灣的某小島，外形酷似橄欖球，如圖1所示．
如圖2所示，現(xiàn)把海岸線近似看作直線m,小島面對海岸線一側(cè)的外緣近似看作AB，經(jīng)測量，AB的長可近似為250π海里，它所對的圓心角（∠AOB）的大小可近似為90°．（注：AB在m上的正投影為圖中線段CD，點(diǎn)O在m上的正投影落在線段CD上．）
（1）求的半徑r；?AB
（2）因該島四面環(huán)海，淡水資源缺乏，為解決島上居民飲用淡水難的問題，擬在海岸線上，建造一個(gè)淡水補(bǔ)給站，向島上居民輸送淡水．為節(jié)約運(yùn)輸成本，要求補(bǔ)給站到小島外緣AB的距離最近（即，要求補(bǔ)給站與上的任意一點(diǎn)，兩點(diǎn)之間的距離取得最小值．）；?AB
請你依據(jù)所學(xué)幾何知識(shí)，在圖2中畫出補(bǔ)給站位置及最短運(yùn)輸路線．（保留畫圖痕跡，并做必要標(biāo)記與注明；不限于尺規(guī)作圖，不要求證明．）
（3）如圖3，若測得AC長為600海里，BD長為500海里，試求出（2）中的最小距離．發(fā)布：2025/5/22 20:30:1組卷：763引用：1難度：0.4 -
2．定義，若四邊形的一條對角線平分這個(gè)四邊形的面積，則稱這個(gè)四邊形為倍分四邊形，這條對角線稱為這個(gè)四邊形的倍分線．如圖①，在四邊形ABCD中，若S△ABC=S△ADC，則四邊形ABCD為倍分四邊形，AC為四邊形ABCD的倍分線．
（1）判斷：若是真命題請?jiān)诶ㄌ?hào)內(nèi)打√，若是假命題請?jiān)诶ㄌ?hào)內(nèi)打×．
①平行四邊形是倍分四邊形．
②梯形是倍分四邊形．
（2）如圖①，倍分四邊形ABCD中，AC是倍分線，若AC⊥AB，AB=3，AD=DC=5，求BC；
（3）如圖②，△ABC中BA=BC，以BC為直徑的⊙O分別交AB、AC于點(diǎn)N、M，已知四邊形BCMN是倍分四邊形．
①求sinC；
②連結(jié)BM，CN交于點(diǎn)D，取OC中點(diǎn)F，連結(jié)MF交NC于E（如圖③），若OF=3，求DE．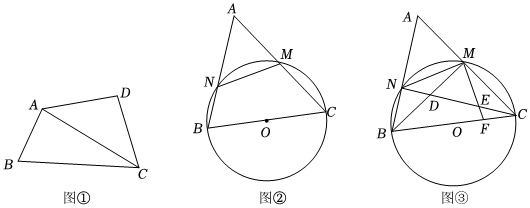
發(fā)布：2025/5/22 21:0:1組卷：1287引用：3難度：0.1 -
3．在平面直角坐標(biāo)系xOy中，對于線段AB，點(diǎn)P和圖形G定義如下：線段AB繞點(diǎn)P逆時(shí)針旋轉(zhuǎn)90°得到線段A'B'（A'和B'分別是A和B的對應(yīng)點(diǎn)），若線段AB和A'B'均在圖形G的內(nèi)部（包括邊界），則稱圖形G為線段AB關(guān)于點(diǎn)P的旋垂閉圖．
（1）如圖，點(diǎn)C（1，0），D（3，0）．
①已知圖形G1：半徑為3的⊙O；
G2：以O(shè)為中心且邊長為6的正方形；
G3：以線段OD為邊的等邊三角形．
在G1，G2，G3中，線段CD關(guān)于點(diǎn)O的旋垂閉圖是 ．
②若半徑為5的⊙O是線段CD關(guān)于點(diǎn)T（t,0）的旋垂閉圖，求t的取值范圍；
（2）已知長度為4的線段AB在x軸負(fù)半軸和原點(diǎn)組成的射線上，若存在點(diǎn)Q（2+a,2-a），使得對半徑為2的⊙Q上任意一點(diǎn)P，都有線段AB滿足半徑為r的⊙O是該線段關(guān)于點(diǎn)P的旋垂閉圖，直接寫出r的取值范圍．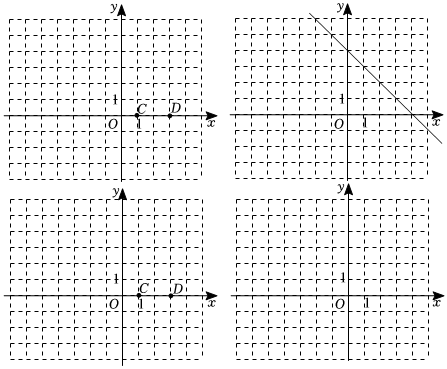
發(fā)布：2025/5/22 21:0:1組卷：275引用：6難度：0.3
相關(guān)試卷