閱讀下面的材料：
【材料一】若m2-2mn+2n2-8n+16=0，求m,n的值．
解：∵m2-2mn+2n2-8n+16=0，
∴（m2-2mn+n2）+（n2-8n+16）=0，
∴（m-n）2+（n-4）2=0，
∴（m-n）2=0，（n-4）2=0，
∴n=4，m=4．
【材料二】“a≥0”這個結論在數學中非常有用，有時我們需要將代數式配成完全平方式．例如：m2+8m+17=m2+8m+16+1=（m+4）2+1．
∵（m+4）2≥0，
∴（m+4）2+1≥1，
∴m2+8m+17≥1．
故m2+8m+17有一個最小值為1．
閱讀材料，探究下列問題：
（1）已知x2-2xy+2y2+6y+9=0，求xy的值；
（2）無論m取何值，代數式m2+6m+13總有一個最小值，求出它的最小值．
【考點】配方法的應用；非負數的性質：偶次方．
【答案】（1）9；
（2）4．
（2）4．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/9 11:30:1組卷：384引用：4難度：0.7
相似題
-
1．閱讀理解：我們知道，“作差法”是比較兩數（式）大小關系常用的方法之一，其依據是不等式（或等式）的性質：若x-y＞0，則x＞y；若x-y=0，則x=y；若x-y＜0，則x＜y.
例：已知A=m2+2mn,B=4mn-n2，其中m≠n,求證：A＞B．
證明：
A-B=（m2+2mn）-（4mn-n2）=m2+2mn-4mn+n2=m2-2mn+n2=（m-n）2．
∵m≠n,∴（m-n）2＞0．∴A＞B．
（1）比較大小：x2+4 4x；
（2）已知M=2019×2022，N=2020×2021，試運用上述方法比較M、N的大小，并說明理由；
（3）應用拓展
學科內應用：①請以“作差法”為研究不等關系的出發點，嘗試證明不等式具有如下性質：如果a＞b,c＞d,那么a+c＞b+d.
②嘗試用：①問的性質解決以下問題：
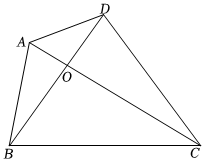
已知：四邊形ABCD是任意四邊形，AC與BD交于點O．求證：AC+BD＞（AB+BC+CD+DA）．12
生活中應用：③某游泳館在暑假期間對學生優惠開放，有A、B兩種方案可供選擇，A方案每次按原票價打八五折；B方案第一次按原票價，但從第二次起，每次打八折，請問游泳的同學選擇哪種方案更合算？發布：2025/6/9 8:0:1組卷：135引用：1難度：0.5 -
2．已知a、b、c滿足a+b=5，c2=ab+b-9，則ab-c=．
發布：2025/6/9 3:0:1組卷：238引用：3難度：0.7 -
3．已知a、b、c滿足a2+2b=7，b2-2c=-1，c2-6a=-17，則（b-c）2=．
發布：2025/6/9 3:30:1組卷：183引用：1難度：0.6