綜合與實踐.
在一次綜合實踐活動課上,數學王老師給每位同學各發了一張正方形紙片,要求同學們僅通過折紙的方法來確定該正方形一邊上的一個三等分點.
“啟航”小組的同學在經過一番思考和討論交流后,進行了如下的操作:
第一步:如圖1,將正方形紙片ABCD的一條邊AD對折,使點A和點D重合,得到AD的中點E,然后展開鋪平;
第二步:如圖2,將CD邊沿CE翻折到CF的位置;
第三步:如圖3,再將BC沿過點C的直線翻折,使點B和點F重合,折痕與AB邊交于點G.
他們認為:該點G就是AB邊的一個三等分點.
(1)試證明上面的結論:
(2)“奮進”小組的同學是這樣操作的:
第一步:先將正方形紙片ABCD的一條邊AD對折,使點A和點D重合,找到AD的中點E;
第二步:再折出正方形紙片ABCD的對角線AC,以及點B和點E的連線BE,這兩條折痕相交于點F;
第三步:最后,過點F折出AB的平行線GN,分別與AD,BC交于點G和點N.
①請根據上面的描述,在圖4中畫出所有的折痕,確定點G和點N的位置;
②請結合①中所畫的圖形,判斷點G是否為AD邊的三等分點,并說明理由.

【考點】四邊形綜合題.
【答案】(1)證明過程見解答;
(2)①圖形見解答;
②點G是AD邊的三等分點.理由見解答.
(2)①圖形見解答;
②點G是AD邊的三等分點.理由見解答.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:242引用:1難度:0.1
相似題
-
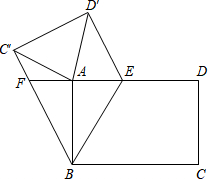 1.如圖,在矩形ABCD中,AB=4,AD=6,E是AD邊上的一個動點,將四邊形BCDE沿直線BE折疊,得到四邊形BC′D′E,連接
1.如圖,在矩形ABCD中,AB=4,AD=6,E是AD邊上的一個動點,將四邊形BCDE沿直線BE折疊,得到四邊形BC′D′E,連接
AC′,AD′.
(1)若直線DA交BC′于點F,求證:EF=BF;
(2)當AE=時,求證:△AC′D′是等腰三角形;433
(3)在點E的運動過程中,求△AC′D′面積的最小值.發布:2025/5/24 17:0:2組卷:632引用:3難度:0.1 -
2.如圖(1),已知矩形ABCD中,AB=6cm,BC=
cm,點E為對角線AC上的動點.連接BE.過E作EB的垂線交CD于點F.23
(1)探索BE與EF的數量關系,并說明理由.
(2)如圖(2),過F作AC的垂線交AC于點G,交EB于點H,連接CH.若點E從
A出發沿AC方向以cm/s的速度向終點C運動,設E的運動時間為t s.23
①是否存在t,使得H與B重合?若存在,求出t的值;若不存在,說明理由;
②t為何值時,△CFH是等腰三角形;
③當CG=GH時,求△CGH的面積.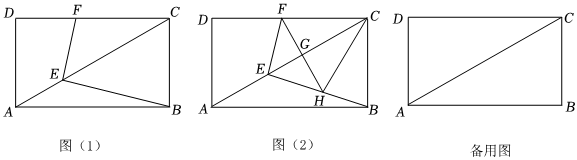 發布:2025/5/24 17:30:1組卷:221引用:1難度:0.2
發布:2025/5/24 17:30:1組卷:221引用:1難度:0.2 -
3.如圖,在正方形ABCD中,AB=6,E為AB的中點,連結CE,作CF⊥EC交射線AD于點F,過點F作FG∥CE交射線CD于點G,連結EG交AD于點H.
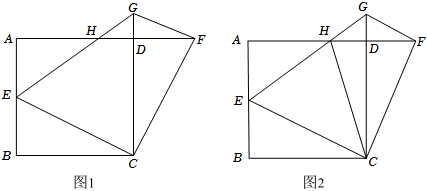
(1)求證:CE=CF.
(2)求HD的長.
(3)如圖2,連結CH,點P為CE的中點,Q為AF上一動點,連結PQ,當∠QPC與四邊形GHCF中的一個內角相等時,求所有滿足條件的DQ的長.發布:2025/5/24 18:0:1組卷:789引用:2難度:0.1


