某超市從廠家購進A、B兩種型號的水杯，兩次購進水杯的情況如表：
| 進貨批次 | A型水杯（個） | B型水杯（個） | 總費用（元） |
| 一 | 100 | 200 | 8000 |
| 二 | 200 | 300 | 13000 |
（2）在銷售過程中，A型水杯因為物美價廉而更受消費者喜歡．為了增大B型水杯的銷售量，超市決定對B型水杯進行降價銷售，當銷售價為44元時，每天可以售出20個，每降價1元，每天將多售出5個，請問超市應將B型水杯降價多少元時，每天售出B型水杯的利潤達到最大？最大利潤是多少？
（3）第三次進貨用10000元錢購進這兩種水杯，如果每銷售出一個A型水杯可獲利10元，售出一個B型水杯可獲利9元，超市決定每售出一個A型水杯就為當地“新冠疫情防控”捐b元用于購買防控物資．若A、B兩種型號的水杯在全部售出的情況下，捐款后所得的利潤始終不變，此時b為多少？利潤為多少？
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1553引用：7難度：0.6
相似題
-
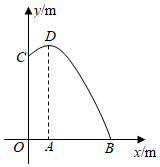1．某景點的“噴水巨龍”口中C處的水流呈拋物線形，該水流噴出的高度y（m）與水平距離x（m）之間的關系如圖所示，D為該水流的最高點，DA⊥OB，垂足為A．已知OC=OB=8m,OA=2m,則該水流距水平面的最大高度AD的長度為（ ）發布：2025/5/25 19:30:2組卷：3237引用：11難度：0.7 -
2．“慈母手中線，游子身上衣”，為感恩母親，許多子女選擇用康乃馨這種鮮花來表達對母親的祝福，某花店采購了一批康乃馨，進價是每支8元．當每支售價為12元時，可銷售30支；當每支售價為10元時，可銷售40支，在銷售過程中，發現這種康乃馨的銷售量y（支）是每支售價x（元）的一次函數（0≤x＜30）．
（1）求y與x之間的函數關系式；
（2）設此花店這種康乃馨的銷售利潤是w元，根據題意：當銷售單價為多少元時，商家獲得利潤最大．發布：2025/5/25 20:0:1組卷：216引用：2難度：0.6 -
3．貧困戶李大爺在某單位精準扶貧工作隊的幫扶下，將一片坡地改造后種植了優質水果藍莓，經核算，種植成本為18元/千克．今年正式上市銷售，通過30天的試銷發現：①第1天賣出20千克，以后每天比前一天多賣4千克：②銷售價格y（元/千克）與時間x（天）之間滿足如下函數關系：y=
，且第12天的售價為32元/千克，第23天的售價為25元/千克．mx-76m（1≤x＜20，x為正整數）n（20≤x≤30，x為正整數）
（1）填空：m=，n=；試銷中銷售量P（千克）與時間x（天）之間的函數關系式為 ；
（2）求銷售藍莓第幾天時，當天的利潤W最大？最大利潤是多少元？
（3）求試銷的30天中，當天利潤W不低于870元的天數共有幾天？發布：2025/5/25 20:30:1組卷：388引用：1難度：0.3