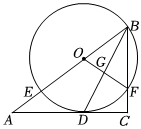
如圖，在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于點D，O為BA上一點，經(jīng)過點B，D的⊙O分別交AB，BC于點E，F(xiàn)，連接OF交BD于點G．
（1）求證：AC是⊙O的切線；
（2）求證：BD2=BA?BF；
（3）若AE=5，sinA=35，求BD的長．
3
5
【考點】圓的綜合題．
【答案】（1）證明見解析；
（2）證明見解析；
（3）6．
（2）證明見解析；
（3）6
5
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：502引用：4難度：0.4
相似題
-
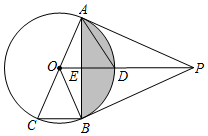1．如圖，PA、PB是⊙O的切線，A、B是切點，AC是⊙O的直徑，連接OP，交⊙O于點D，交AB于點E．
（1）求證：BC∥OP；
（2）若E恰好是OD的中點，且四邊形OAPB的面積是16，求陰影部分的面積；3
（3）若sin∠BAC=，且AD=213，求切線PA的長．3發(fā)布：2025/5/23 16:0:1組卷：2045引用：7難度：0.1 -
2．【問題提出】
（1）如圖①，AB為⊙O的一條弦，圓心O到弦AB的距離為4，若⊙O的半徑為7，則⊙O上的點到弦AB的距離最大值為 ；
【問題探究】
（2）如圖②，在△ABC中，∠BAC=60°，AD為BC邊上的高，若AD=6，求△ABC面積的最小值；
【問題解決】
（3）“雙減”是黨中央、國務院作出的重大決策部署，實施一年多來，工作進展平穩(wěn)，取得了階段性成效，為了進一步落實雙減政策，豐富學生的課余生活，某校擬建立一塊綜合實踐基地，如圖③，△ABC為基地的大致規(guī)劃示意圖，其中∠ABC=90°，BD平分∠ABC交AC于點D，點P為BC上一點，學校計劃將四邊形ABPD部分修建為農(nóng)業(yè)實踐基地，并沿BD鋪設(shè)一條人行走道，△CDP部分修建為興趣活動基地．根據(jù)規(guī)劃要求，米，∠CDP=45°．且農(nóng)業(yè)實踐基地部分（四邊形ABPD）的面積應盡可能小，問四邊形ABPD的面積是否存在最小值？若存在，求出其最小值；若不存在，請說明理由．BD=802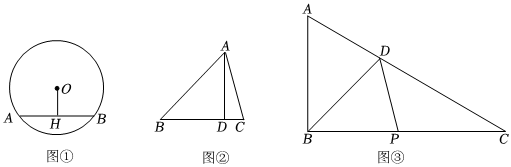
發(fā)布：2025/5/23 16:0:1組卷：251引用：1難度：0.3 -
3．AB、AC為圓O的弦，OA平分∠BAC．
（1）如圖1，求證：弧AB=弧AC；
（2）如圖2，連接BO并延長交圓O于點F，連接AF，作BG⊥AC于點G，延長AO交BG于點M，求證：AF=BM；
（3）如圖3，在（2）的條件下，連接OG，延長BG交圓O于點D，連接CD并延長，與AF的延長線交于點K，AB=2FK，BC=6，求OG的長．
發(fā)布：2025/5/23 16:30:1組卷：112引用：1難度：0.2
相關(guān)試卷