如圖，在梯形ABCD中，∠B=90°，AD∥BC，AD=20cm,AB=8cm,BC=26cm,動點P從A點開始沿AD邊向D以1cm/秒的速度運動，動點Q從C點開始沿CB邊向B以3cm/秒的速度運動，P、Q分別從A、C同時出發(fā)，當其中一點到墻點時，另一點也隨之停止運動，設(shè)運動時間為t秒．問：
（1）求t為何值時，四邊形PQCD是平行四邊形？
（2）四邊形ABQP可能是矩形嗎？如果可能，求出t的值；如果不可能，說明理由；
（3）四邊形PQCD可能是菱形嗎？如果可能，求出t的值；如果不可能，說明理由．
【考點】四邊形綜合題．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：118引用：5難度：0.3
相似題
-
1．（1）【問題發(fā)現(xiàn)】
如圖1，在Rt△ABC中，AB=AC，∠BAC=90°，點D為BC的中點，以CD為一邊作正方形CDEF，點E恰好與點A重合，則線段BE與AF的數(shù)量關(guān)系為．
（2）【拓展探究】
在（1）的條件下，如果正方形CDEF繞點C旋轉(zhuǎn)，請判斷線段BE與AF的數(shù)量關(guān)系，并就圖2的情形說明理由．
（3）【問題解決】
當AB=AC=2，且第（2）中的正方形CDEF旋轉(zhuǎn)到B，E，F(xiàn)三點共線時，請直接寫出線段AF的長．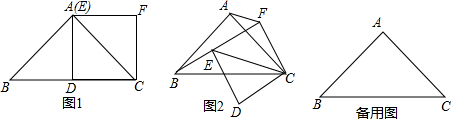
發(fā)布：2025/5/24 21:30:1組卷：328引用：4難度：0.2 -
2．知識再現(xiàn)：已知，如圖1，四邊形ABCD是正方形，點M、N分別在邊BC、CD上，連接AM、AN、MN，且∠MAN=45°，延長CB至G使BG=DN，連接AG，根據(jù)三角形全等的知識，我們可以證明MN=BM+DN．
知識探究：（1）如圖1，作AH⊥MN，垂足為點H，猜想AH與AB有什么數(shù)量關(guān)系？并進行證明．
知識運用：（2）如圖2，四邊形ABCD是正方形，E是邊BC的中點，F(xiàn)為邊CD上一點，且∠FEC=2∠BAE，AB=24，求DF的長．
知識拓展：（3）已知∠BAC=45°，AD⊥BC于點D，且BD=2，AD=6，求CD的長．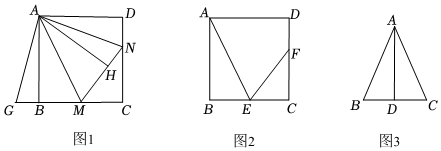
發(fā)布：2025/5/24 21:0:1組卷：268引用：2難度：0.4 -
3．已知：線段EF和矩形ABCD如圖①擺放（點E與點B重合），點F在邊BC上EF=1cm,AB=4cm,BC=8cm.如圖②．EF從圖①的位置出發(fā)，沿BC方向運動，速度為1cm/s；動點P同時從點D出發(fā)，沿DA方向運動，速度為1cm/s.點M為AB的中點，連接PM，ME，DF，PM與AC相交于點Q，設(shè)運動時間為（s）（0＜1≤7）．解答下列問題：
（1）當PM⊥AC時，求r的值；
（2）設(shè)五邊形PMEFD的面積為S（cm2），求S與t的關(guān)系式；
（3）當ME∥AC時，求線段AQ的長；
（4）當t為何值時，五邊形DAMEF的周長最小，最小是多少？直接寫出答案即可）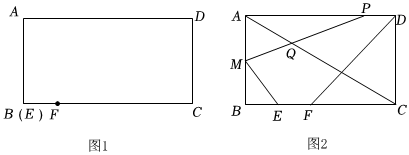
發(fā)布：2025/5/24 21:0:1組卷：133引用：1難度：0.1
相關(guān)試卷