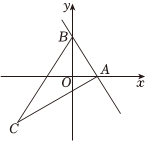
如圖所示，已知直線y=kx+2與x軸的正半軸交于點(diǎn)A（t,0），與y軸交于點(diǎn)B，拋物線y=-x2+bx+c經(jīng)過(guò)點(diǎn)A與點(diǎn)B，點(diǎn)C在第三象限內(nèi)，且AC⊥AB，tan∠ABC=2．
（1）當(dāng)t=1時(shí)，求拋物線的表達(dá)式；
（2）設(shè)點(diǎn)C坐標(biāo)為（x,y），試用t分別表示x,y；
（3）記Z=xy,求Z的最大值．
【考點(diǎn)】二次函數(shù)的性質(zhì)與圖象．
【答案】（1）y=-x2-x+2；
（2）x=t-4，y=-2t；
（3）8．
（2）x=t-4，y=-2t；
（3）8．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/3 8:0:9組卷：21引用：2難度：0.6
相似題
-
1．方程ay=b2x2+c中的a,b,c∈{-3，-2，0，1，2，3}，且a,b,c互不相同，在所有這些方程所表示的曲線中，不同的拋物線共有條．
發(fā)布：2024/12/29 11:30:2組卷：95引用：5難度：0.5 -
2．下列命題是真命題的是（ ）
發(fā)布：2025/1/5 19:30:5組卷：147引用：3難度：0.7 -
3．園林工人計(jì)劃使用可以做出20m柵欄的材料，在靠墻的位置圍出一塊矩形的花圃．要使得花圃的面積不小于42m2，你能確定與墻平行的柵欄的長(zhǎng)度范圍嗎？
發(fā)布：2025/1/2 18:30:1組卷：3引用：1難度：0.5