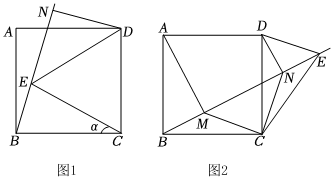
如圖，已知正方形ABCD，將邊CB繞點C順時針旋轉α得到CE，連接BE并延長，過點D作DN⊥射線BE于點N，連接DE．
（1）如圖1，當α=30°時，求∠CED和∠EDN的度數；
（2）如圖2，當90°＜α＜180°時，過點A作AM⊥BE于點M．連接CM，CN．
①證明：ND=NE；
②在CE的旋轉過程中，是否存在△CMN與△NDE相似？若存在，求出tan∠CBM的值：若不存在，請說明理由．
【考點】相似形綜合題．
【答案】（1）45°；
（2）①見解析；
②．
（2）①見解析；
②
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：290引用：1難度：0.3
相似題
-
1．【問題情境】
（1）古希臘著名數學家歐幾里得在《幾何原本》提出了射影定理，又稱“歐幾里德定理”：在直角三角形中，斜邊上的高是兩條直角邊在斜邊射影的比例中項，每一條直角邊又是這條直角邊在斜邊上的射影和斜邊的比例中項．射影定理是數學圖形計算的重要定理．
其符號語言是：如圖1，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足為D，則：（1）CD2=AD?BD，（2）AC2=AB?AD，（3）BC2=AB?BD；請你證明定理中的結論（3）BC2=AB?BD．
【結論運用】
（2）如圖2，正方形ABCD的邊長為6，點O是對角線AC、BD的交點，點E在CD上，過點C作CF⊥BE，垂足為F，連接OF，
①求證：△BOF∽△BED；
②若BE=2，求OF的長．10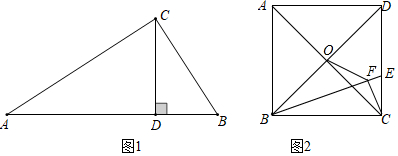
發布：2025/5/22 0:0:2組卷：1315引用：5難度：0.3 -
2．閱讀材料：三角形的三條中線必交于一點，這個交點稱為三角形的重心．
（1）特例感知：如圖（1），已知邊長為2的等邊△ABC的重心為點O，則△OBC的面積為；33
（2）性質探究：如圖（2），已知△ABC的重心為點O，對于任意形狀的△ABC，是不是定值，如果是，請求出定值為多少，如果不是，請說明理由；ODOA
（3）性質應用：如圖（3），在任意矩形ABCD中，點E是CD的中點，連接BE交對角線AC于點M，的值是不是定值，如果是，請求出定值為多少，如果不是，請說明理由；S矩形ABCDS三角形CME
（4）思維拓展：如圖（4），∠MON=30°，N點的坐標為（2，0），M點的坐標為（3，），點Q在線段OM上以每秒1個單位的速度由O向M點移動，當Q運動到M點就停止運動，連接NQ，將△MON分為△OQN和△MQN兩個三角形，當其中一個三角形與原△MON相似時，求點Q運動的時間t.3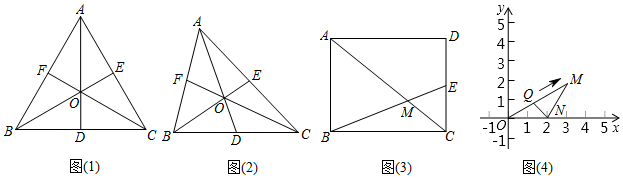
發布：2025/5/22 1:0:1組卷：617引用：4難度：0.1 -
3．如圖，等腰Rt△ABC，∠ACB=90°，分別以AB，AC為邊長在AB同側作等邊△ABD和等邊△ACE，AD與CE相交于點F，連接DE，DC．
（1）求證：BC=DE；
（2）求證：CD2=AC?FC；
（3）已知AB=2，求線段EF的長．發布：2025/5/22 2:30:1組卷：144引用：4難度：0.1