在菱形ABCD中，∠BAD=α，E為對角線AC上的一點（不與A，C重合），將射線EB繞點E順時針旋轉β角之后，所得射線與直線AD交于F點．試探究線段EB與EF的數量關系．
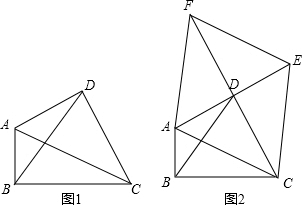
（1）如圖1，當α=β=90°時，EB與EF的數量關系為 EB=EFEB=EF；
（2）如圖2，當α=60°，β=120°時，
①依題意補全圖形；
②請幫小宇繼續探究（1）的結論是否成立．若成立，請給出證明；若不成立，請舉出反例說明；
（3）在此基礎上對一般的圖形進行了探究，設∠ABE=γ，若旋轉后所得的線段EF與EB的數量關系滿足（1）中的結論，請直接寫出角α，β，γ滿足的關系：當點F落在點D處時，12α+12β+γ=180°，其他情況：無論γ為多少度時，α+β=180°當點F落在點D處時，12α+12β+γ=180°，其他情況：無論γ為多少度時，α+β=180°．
1
2
1
2
1
2
1
2
【考點】四邊形綜合題．
【答案】EB=EF；當點F落在點D處時，α+β+γ=180°，其他情況：無論γ為多少度時，α+β=180°
1
2
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：32引用：1難度：0.1
相似題
-
1．定義：只有一組對角是直角的四邊形叫做損矩形，連接它的兩個非直角頂點的線段叫做這個損矩形的直徑．如圖1，∠ABC=∠ADC=90°，四邊形ABCD是損矩形，則該損矩形的直徑是線段AC．同時我們還發現損矩形中有公共邊的兩個三角形角的特點：在公共邊的同側的兩個角是相等的．如圖1中：△ABC和△ABD有公共邊AB，在AB同側有∠ADB和∠ACB，此時∠ADB=∠ACB；再比如△ABC和△BCD有公共邊BC，在CB同側有∠BAC和∠BDC，此時∠BAC=∠BDC．
（1）請在圖1中再找出一對這樣的角來：=．
（2）如圖2，△ABC中，∠ABC=90°，以AC為一邊向外作菱形ACEF，D為菱形ACEF對角線的交點，連接BD，當BD平分∠ABC時，判斷四邊形ACEF為何種特殊的四邊形？請說明理由．
（3）在第（2）題的條件下，若此時AB=6，BD=8，求BC的長．2發布：2025/6/8 10:0:2組卷：584引用：6難度：0.3 -
2．如圖，在長方形OABC中，O為平面直角坐標系的原點，點A坐標為（a,0），點C的坐標為（0，b），且a、b滿足+|b-8|=0，點B在第一象限內，點P從原點出發，以每秒2個單位長度的速度沿著O-C-B-A-O的線路移動．a-4
（1）求a,b的值，點B的坐標．
（2）當點P移動4.5秒時，請指出點P的位置，并求出點P的坐標；
（3）在O-C-B段的移動過程中，當△OPB的面積是12時，求點P移動的時間．發布：2025/6/8 9:30:1組卷：123引用：3難度：0.1 -
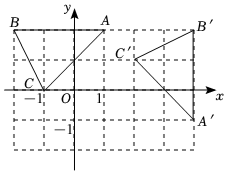3．如圖，在平面直角坐標系中，△ABC繞旋轉中心順時針旋轉90°后得到△A'B'C'，
（1）其旋轉中心的坐標是 ；
（2）寫出點C掃過的路徑長 ；
（3）若在平面內有一點D，且四邊形ABCD是平行四邊形，則該四邊形的周長為 ；
（4）在坐標軸上有點E，使S△ABC=S△AEC，直接寫出E點坐標 （寫出平面內所有符合條件的點坐標）．發布：2025/6/8 10:0:2組卷：81引用：2難度：0.3