對于一個圖形,通過兩種不同的方法計算它的面積,可以得到一個數(shù)學(xué)等式,請解答下列問題.
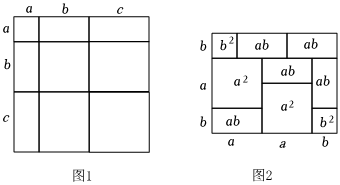
(1)寫出圖1中所表示的數(shù)學(xué)等式 a2+ab+ac+ab+b2+bc+ac+bc+c2=(a+b+c)(a+b+c)a2+ab+ac+ab+b2+bc+ac+bc+c2=(a+b+c)(a+b+c);
(2)利用(1)中得到的結(jié)論,解決下面的問題:若a+b+c=10,a2+b2+c2=30,求ab+ac+bc的值;
(3)請利用圖2的面積,寫出一個數(shù)學(xué)等式 (2b+a)(2a+b)=2b2+5ab+2a2.(2b+a)(2a+b)=2b2+5ab+2a2..
【考點】因式分解的應(yīng)用;完全平方公式的幾何背景.
【答案】a2+ab+ac+ab+b2+bc+ac+bc+c2=(a+b+c)(a+b+c);(2b+a)(2a+b)=2b2+5ab+2a2.
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/9/12 12:0:9組卷:83引用:1難度:0.5
相似題
-
1.對于一個各數(shù)位上的數(shù)字均不為0的三位自然數(shù)p,將它各個數(shù)位上的數(shù)字平方后再取其個位,得到三個新的數(shù)字;再將這三個新數(shù)字重新組合成三位數(shù)
,當(dāng)|x+2y-z|的值最小時,稱此時的xyz為自然數(shù)p的理想數(shù),并規(guī)定K(p)=(x-z)2+y,例如245,各數(shù)字平方后取個位分別為4,6,5,再重新組合為465,456,546,564,654,645,因為|5+2×4-6|=7最小,所以546是原三位數(shù)245的理想數(shù),此時K(p)=(5-6)2+4=5;xyz
若一個三位正整數(shù)的十位數(shù)字是個位數(shù)字的2倍,則稱這個數(shù)為自信數(shù),例如384,其中8=4×2,所以384是自信數(shù);對于一個各數(shù)位上的數(shù)字均不為0三位正整數(shù)p,把它的個位數(shù)字和百位數(shù)字交換所得的新三位數(shù)記為p1,把它的個位數(shù)字和十位數(shù)字交換所得到的新三位數(shù)記為p2,若p1,p2,p這三個數(shù)的和能被29整除,則稱這個數(shù)p為成功數(shù).若一個成功數(shù)p也是自信數(shù),求所以符合條件的成功數(shù)中K(p)的最小值.發(fā)布:2025/5/24 19:30:1組卷:64引用:1難度:0.4 -
2.已知a-b=-l,則3a2-6ab+3b2=.
發(fā)布:2025/5/24 17:0:2組卷:6引用:1難度:0.6 -
3.對于各位數(shù)字都不為0的兩位數(shù)m和三位數(shù)n,將m中的任意一個數(shù)字作為一個新的兩位數(shù)的十位數(shù)字,將n中的任意一個數(shù)字作為該新數(shù)的兩位數(shù)的個位數(shù)字,按照這種方式產(chǎn)生的所有新的兩位數(shù)的和記為F(m,n),例如:F(12,345)=13+14+15+23+24+25=114
(1)F(24,579)=,并求證:當(dāng)n能被3整除時,F(xiàn)(m,n)一定能被6整除;
(2)若一個兩位數(shù)s=21x+y,一個三位數(shù)t=12x+y+198(其其中1≤x≤4,1≤y≤5,且x、y均為整數(shù)).交換三位數(shù)t的百位數(shù)字和個位數(shù)字得到新數(shù)t′,當(dāng)t′與s的個位數(shù)字的3倍的和被7除余1時,稱這樣的兩個數(shù)s和t為“幸運數(shù)對”,求所有“幸運數(shù)對”中F(s,t)的最大值.發(fā)布:2025/5/24 20:30:2組卷:90引用:1難度:0.4


