綜合與實踐.
學習整式乘法時,老師拿出三種型號的卡片,如圖1,A型卡片是邊長為a的正方形,B型卡片是邊長為b的正方形,C型卡片是長和寬分別為a,b的長方形.
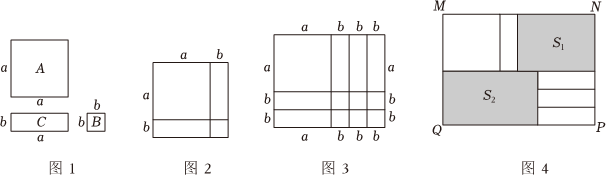
(1)選取1張A型卡片,2張C型卡片,1張B型卡片,在紙上按照圖2的方式拼成一個邊長為(a+b)的大正方形,通過用不同方式表示大正方形的面積,可得到乘法公式 (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2.
(2)圖3是由若干張A,B,C三種卡片拼成的一個長方形,觀察圖形,可將多項式a2+5ab+6b2分解因式為 (a+3b)(a+2b)(a+3b)(a+2b).
(3)選取1張A型卡片,4張C型卡片按圖4的方式不重疊地放在長方形MNPQ框架內,已知NP的長度固定不變,MN的長度可以變化,圖中兩陰影部分(長方形)的面積分別表示為S1,S2,若Q=S1-S2,且Q為定值,則a與b有什么關系?請說明理由.
【答案】(a+b)2=a2+2ab+b2;(a+3b)(a+2b)
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/26 4:0:1組卷:1314引用:6難度:0.5
相似題
-
1.已知2x+y=1,則4x2-y2+2y+5=.
發布:2025/5/21 15:30:1組卷:166引用:2難度:0.6 -
2.若2a-3b=-1,則代數式4a2-6ab+3b的值為.
發布:2025/5/21 12:30:1組卷:2156引用:18難度:0.6 -
3.閱讀理解:
能被7(或11或13)整除的特征:如果一個自然數末三位所表示的數與末三位以前的數字所表示的數之差(大數減小數)是7(或11或13)的倍數,則這個數就能被7(或11或13)整除.
如:456533,533-456=77,77是7的11倍,所以,456533能被7整除.又如:345548214,345548-214=345334,345-334=11,11是11的1倍,所以,345548214能被11整除.
(1)用材料中的方法驗證67822615是7的倍數(寫明驗證過程);
(2)若對任意一個七位數,末三位所表示的數與末三位以前的數字所表示的數之差(大數減小數)是11的倍數,證明這個七位數一定能被11整除.發布:2025/1/5 8:0:1組卷:135引用:3難度:0.4


