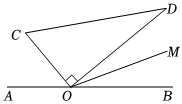
如圖，平面內點O為直線AB上一點，一直角三角板COD（∠COD=90°）的
直角頂點與O重合，OM平分∠BOD，設∠AOC=α．（本題中所有角均小于等于180°）．
（1）如圖，請直接寫出∠AOM=135°+12α135°+12α（用含α的式子表示）；
（2）若圖中α=50°，三角板COD從圖中的位置出發，繞O點以每秒5°的速度順時針旋轉，同時ON從OA出發，以每秒2°的速度逆時針旋轉．設運動時間為t秒（0＜t＜30）．
①當t為何值時，∠AOM+∠CON=270°？
②是否存在一負數k,使得∠AOM+k∠CON取值與t無關．若存在，求此時k的值；若不存在，說明理由．
1
2
α
1
2
α
【答案】135°+
1
2
α
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：2287引用：2難度：0.3
相似題
-
1．已知：一條射線OA，若從點O再引兩條射線OB、OC，使∠AOB=60°，∠BOC=20°，則∠AOC=度．
發布：2025/5/28 9:30:2組卷：611引用：9難度：0.5 -
2．已知∠AOB=90°，OC為一射線，OM，ON分別平分∠BOC和∠AOC，則∠MON的大小為．
發布：2025/5/28 8:0:1組卷：162引用：1難度：0.5 -
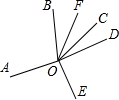3．如圖，從點O引出6條射線OA、OB、OC、OD、OE、OF，且∠AOB=100°，OF平分∠BOC，∠AOE=∠DOE，∠EOF=140°，求∠COD的度數．發布：2025/5/28 5:0:1組卷：327引用：3難度：0.5