如圖，在Rt△ABC中，∠ACB=90°，AC=
2
，將其繞B點順時針旋轉一周，則分別以BA、BC為半徑的圓形成一個圓環，則該圓環的面積為（　　）

A．

B．2π

C．4π

D．6π

【考點】勾股定理．

【答案】B

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/5/27 14:0:0組卷：398引用：3難度：0.7

相似題

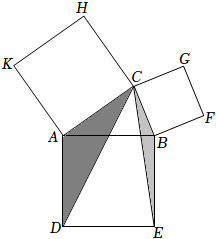1．勾股定理有著悠久的歷史，它曾引起很多人的興趣．現把直角三角形改為銳角三角形：如圖，在銳角△ABC中，以AB，AC，BC為邊分別向外作正方形，連結CD，CE，S_{正方形ACHK}=14，S_{正方形BCGF}=5，記△ADC的面積為S₁，△BCE的面積為S₂，若S₁=4S₂，則正方形ADEB的面積為（　　）
A．15 B．16 C．17 D．18
發布：2025/5/25 17:0:1組卷：348引用：2難度：0.6
解析
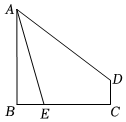2．如圖，在四邊形ABCD中，∠B=∠C=90°，點E在邊BC上，連接AE，若∠BAD-
1
2
∠BAE=45°，AB=BC=4CD，AE=3，則線段AD的長為
．
發布：2025/5/25 22:30:2組卷：866引用：1難度：0.3
解析
3．【閱讀材料】
已知x²-4x=1，求3x²-12x-2的值．
解：∵x²-4x=1，∴原式=3（x²-4x）-2=3×1-2=1．
【初步探究】
已知
1
x
-
1
y
=3，求代數式
2
x
-
14
xy
-
2
y
x
-
2
xy
-
y
的值．
【綜合運用】
在Rt△ABC中，∠C=90°，若AC+BC=23cm,AB=17cm,求Rt△ABC的面積．
發布：2025/5/25 20:0:1組卷：303引用：1難度：0.5
解析

相關試卷

如圖，在Rt△ABC中，∠ACB=90°，AC=2，將其繞B點順時針旋轉一周，則分別以BA、BC為半徑的圓形成一個圓環，則該圓環的面積為（ ）