探究式學習是新課程倡導的重要學習方式，某興趣小組擬做以下探究．
在Rt△ABC中，∠C=90°，AC=BC，D是AB邊上一點，且ADBD=1n（n為正整數），E是AC邊上的動點，過點D作DE的垂線交直線BC于點F．
【初步感知】
（1）如圖1，當n=1時，興趣小組探究得出結論：AE+BF=22AB，請寫出證明過程．
【深入探究】
（2）①如圖2，當n=2，且點F在線段BC上時，試探究線段AE，BF，AB之間的數量關系，請寫出結論并證明；
②請通過類比、歸納、猜想，探究出線段AE，BF，AB之間數量關系的一般結論（直接寫出結論，不必證明）．
【拓展運用】
（3）如圖3，連接EF，設EF的中點為M，若AB=22，求點E從點A運動到點C的過程中，點M運動的路徑長（用含n的代數式表示）．
AD
BD
1
n
2
2
2
【考點】三角形綜合題．
【答案】（1）見解析過程；
（2）①=，見解析過程；
②當點F在射線BC上時，，當點F在CB延長線上時，；
（3）點M運動的路徑長為．
（2）①
①
AE
+
1
2
BF
2
3
AB
②當點F在射線BC上時，
AE
+
1
n
BF
=
2
n
+
1
AB
AE
-
1
n
BF
=
2
n
+
1
AB
（3）點M運動的路徑長為
n
2
+
1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/5 8:0:9組卷：4679引用：5難度：0.1
相似題
-
1．在平面直角坐標系中，點A、B、C的坐標分別為（m,0），（2，-4），（n,0），且m,n滿足方程（m-2）xn-4+
=0為二元一次方程．ym2-3
（1）求A、C的坐標；
（2）若點D為y軸正半軸上的一個動點．
①如圖1，已知∠DAO=∠ACB，∠ADO與∠ACB的角平分線交于點P，求∠P的度數；
②如圖2，連接BD，交x軸于點E．若S△ADE≤S△BCE成立．設動點D坐標為（0，a），求a的取值范圍．
發布：2025/6/8 0:30:1組卷：83引用：1難度：0.1 -
2．在平面直角坐標系中，A（a,0），C（b,2），且滿足（a+b）2+|a-b+4|=0，過C作CB⊥x軸于B．
（1）如圖1，求△ABC的面積．
（2）如圖2，若過B作BD∥AC交y軸于D，在△ABC內有一點E，連接AE、DE，若∠CAE+∠BDE=∠EAO+∠EDO，求∠AED的度數．
（3）如圖3，在（2）的條件下，DE與x軸交于點M，AC與y軸交于點F，作△AME的角平分線MP，在PE上有一點Q，連接QM，∠EAM+2∠PMQ=45°，當AE=mAM，FO=2QM時，求點E的縱坐標（用含m的代數式表示）．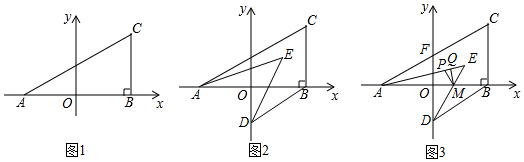
發布：2025/6/7 23:0:2組卷：189引用：2難度：0.2 -
3．已知線段AB⊥l于點B，點D在直線l上，分別以AB、AD為邊作等邊三角形ABC和等邊三角形ADE，直線CE交直線l于點F．
（1）當點F在線段BD上時，如圖①，直接寫出DF，CE，CF之間的關系 ．
（2）當點F在線段BD的延長線上時，如圖②，當點F在線段DB的延長線上時，如圖③，請分別寫出線段DF、CE、CF之間的數量關系，在圖②、圖③中選一個進行證明．
（3）在（1）、（2）的條件下，若BD=2BF，EF=6，請直接寫出CF的值．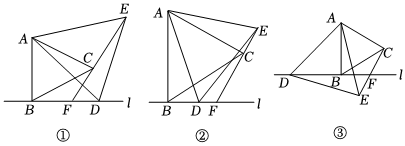
發布：2025/6/8 2:0:5組卷：424引用：2難度：0.1
相關試卷