【課本再現】我們知道：三角形三個內角的和等于180°，利用它我們可以推出結論：三角形的外角等于與它不相鄰的兩個內角的和．
【定理證明】
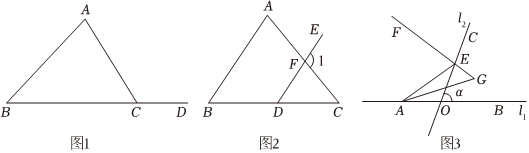
（1）為證明此定理，小紅同學畫好了圖形（如圖1），寫好了“已知”和“求證”，請你完成證明過程．
已知：如圖1，∠ACD是△ABC的一個外角．
求證：∠ACD=∠A+∠B．
【知識應用】
（2）如圖2，在△ABC中，∠C=50°，點D在BC邊上，DE∥AB交AC于點F．∠1=125°，求∠B的度數．
（3）如圖3，直線l1與直線l2相交于點O，夾角α為銳角，點B在直線l1上且在點O右側，點C在直線l2上且在直線l1上方，點A在直線l1上且在點O左側運動，點E在射線CO上運動（不與點C、O重合）．當α=70°時，EF平分∠AEC，AG平分∠EAB交直線EF于點G，求∠G的度數．
【考點】三角形綜合題．
【答案】（1）證明見解析；
（2）75°；
（3）55°或125°．
（2）75°；
（3）55°或125°．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/8 13:0:2組卷：107引用：3難度：0.5
相似題
-
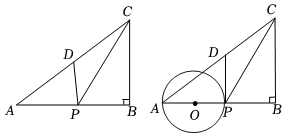1．如圖①，在△ABC中，∠ABC=90°，AC=10，BC=6，D點為AC邊的中點．點P在邊AB上運動（點P不與A、B重合），連結PD、PC．設線段AP的長度為x.
（1）求AB的長．
（2）當△APD是等腰三角形時，求這個等腰三角形的腰長．
（3）連結PD、PC，當PD+PC取最小值時，求x的值．
（4）如圖②，取AP的中點為O，以點O為圓心，以線段AP的長為直徑的圓與線段PD有且只有一個公共點時，直接寫出x的取值范圍．發布：2025/5/26 6:30:2組卷：176引用：1難度：0.3 -
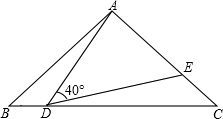2．如圖，在△ABC中，AB=AC=2，∠B=40°，點D在線段BC上運動（D不與B、C重合），連接AD，作∠ADE=40°，DE交線段AC于E．
（1）當∠BDA=115°時，∠BAD=°，∠DEC=°；
（2）當DC等于多少時，△ABD與△DCE全等？請說明理由；
（3）在點D的運動過程中，△ADE的形狀可以是等腰三角形嗎？若可以，請直接寫出∠BDA的度數．若不可以，請說明理由．發布：2025/5/26 2:30:2組卷：976引用：8難度：0.3 -
3．在△ABC中，AB=AC，BC=12，E為邊AC的中點，
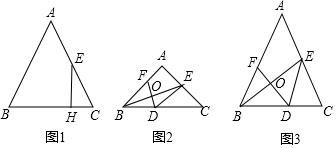
（1）如圖1，過點E作EH⊥BC，垂足為點H，求線段CH的長；
（2）作線段BE的垂直平分線分別交邊BC、BE、AB于點D、O、F．
①如圖2，當∠BAC=90°時，求BD的長；
②如圖3，設tan∠ACB=x,BD=y,求y與x之間的函數表達式和tan∠ACB的最大值．發布：2025/5/26 1:0:1組卷：278引用：2難度：0.1