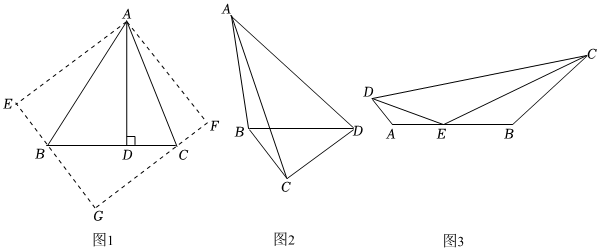
【問題情境】：如圖1，在△ABC中，∠BAC=45°，AD⊥BC于D，BD=3，DC=2，求AD的長．
【問題解決】小明同學是這樣分析的：將△ABD沿著AB翻折得到△ABE，將△ACD 沿著AC翻折得到△ACF，延長EB、FC相交于點G，設AD為x,在Rt△GBC中運用勾股定理，可以求出AD的長．
（1）說明四邊形AEGF是正方形；
（2）求出AD的長．
【方法提煉】請用小明的方法解決以下問題：
（3）如圖2，四邊形ABCD中，∠BAD=45°，BC=6，CD=8，BD=10，求AC的最大值．
（4）如圖3，四邊形ABCD中，BC=6，AD=2，點E是AB上一點，且∠DEC=135°，AE=3，BE=4，則CD的最大值為 1313．（直接寫出結果）
?
【考點】四邊形綜合題．
【答案】13
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/29 8:0:9組卷：281引用：3難度：0.1
相似題
-
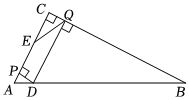1．如圖，在△ABC中，∠C=90°，AC=10，BC=20，點D從點A出發，以每秒個單位長度的速度沿AB方向運動，到點B停止．當點D與A、B兩點不重合時，作DP⊥AC交AC于點P，作DQ⊥BC交BC于點Q．E為射線CA上一點，且∠CQE=∠BAC．設點D的運動時間為t（秒）．5
（1）AB的長為 ．
（2）求CQ的長．（用含有t的代數式表示）
（3）線段QE將矩形PDQC分成兩部分圖形的面積比為1：3時，求t的值．
（4）當t為某個值時，沿PD將以D、E、Q、A為頂點的四邊形剪開，得到兩個圖形，用這兩個圖形拼成不重疊且無縫隙的圖形恰好是三角形．請直接寫出所有符合上述條件的t值．發布：2025/5/23 6:30:1組卷：84引用：2難度：0.1 -
2．（1）感知：如圖①，四邊形ABCD和CEFG均為正方形，BE與DG的數量關系為 ；
（2）拓展：如圖②，四邊形ABCD和CEFG均為菱形，且∠A=∠F，請判斷BE與DG的數量關系，并說明理由；
（3）應用：如圖③，四邊形ABCD和CEFG均為菱形，點E在邊AD上，點G在AD延長線上．若AE=2ED，∠A=∠F，△EBC的面積為8，求菱形CEFG的面積．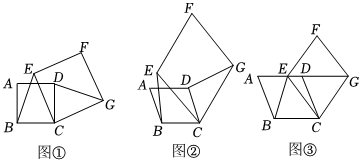
發布：2025/5/23 5:30:3組卷：229引用：1難度：0.3 -
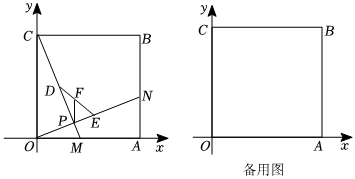3．如圖所示，在平面直角坐標系中，正方形OABC在第一象限，A（8，0）．點M，N分別為邊OA，AB上的動點，且點OM=AN，D，E分別為CM，ON的中點，F是DE的中點．設OM=t,點P的縱坐標為y,請解決下列問題：
（1）判斷CM與ON的位置關系，并寫出證明過程；
（2）請求出y關于t的函數表達式，并直接寫出y最大時，點P的坐標；
（3）在點M從點O運動到點A的過程中，設點F走過的路線長為L，線段PF掃過的面積為S，請直接寫出L與S的值．發布：2025/5/23 6:0:2組卷：77引用：1難度：0.3