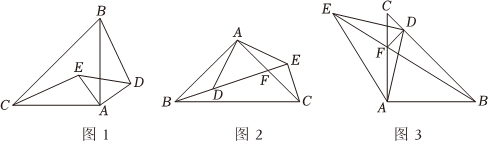
【模型建立】（1）如圖1，在Rt△ABC與Rt△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°，求證：△AEC≌△ADB；
【模型應用】（2）如圖2，在△ABC與△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°，B、D、E三點在一條直線上，AC與BE交于點F，若點F為AC中點，
①求∠BEC的大小；
②CE=3，求△AEF的面積；
【拓展提高】（3）如圖3，在△ABC與△ADE中，AB=AC，DA=DE，∠BAC=∠ADE=90°，BE與CA交于點F，DC=DF，CD⊥DF，△BCF的面積為18，求AF的長．
【考點】三角形綜合題．
【答案】（1）證明見解析過程；
（2）90°；2.25；
（3）6．
（2）90°；2.25；
（3）6．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/6 17:0:2組卷：279引用：3難度：0.1
相似題
-
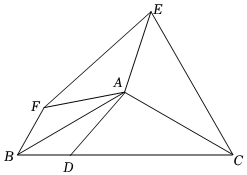1．如圖，已知△ABC，AB=AC，BC=6，∠BAC=120°，點D在BC上（不與B、C重合），連接AD，分別將△ABD和△ACD沿直線AB、AC翻折得到△ABF和△ACE，連接EF，給出下列結論：
①EF=AF；3
②當AD⊥AF時，CD的長為2；3
③當D、A、F三點共線時，四邊形ADCE是菱形；
④△AEF面積的最小值為．334
則正確結論有 ．（填序號）發布：2025/5/22 18:30:2組卷：430引用：2難度：0.2 -
2．將一個直角三角形紙片OAB放置在平面直角坐標系中，點O（0，0），點A（2，0），點
，∠OAB=90°，以點A為中心順時針旋轉△AOB，得到△ACD，點O，B的對應點分別是C，D，記旋轉角為α（0°≤α≤180°）．B（2，23）
（Ⅰ）如圖①，當點C落在OB邊上時，求點C的坐標；
（Ⅱ）如圖②，連接OC，BD，點E，F分別是線段OC，BD的中點，連接AE，AF，EF，若線段OC的長為t,試用含t的式子表示線段AE的長度，并寫出t的取值范圍；
（Ⅲ）在（Ⅱ）的條件下，若△AEF的面積是S，當60°≤α≤120°時，求S的取值范圍（直接寫出結果即可）．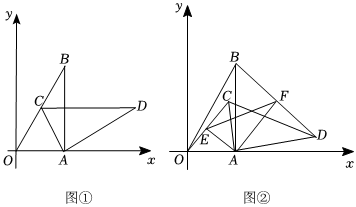
發布：2025/5/22 19:0:1組卷：644引用：1難度：0.2 -
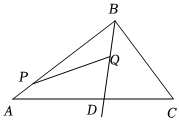3．在Rt△ABC中，∠ABC=90°，AB=4，BC=3，BD平分∠ABC，動點P從點A出發，沿AB以每秒1個單位長度的速度向終點B運動，同時，動點Q從點B出發，沿射線BD以每秒個單位長度的速度運動，當點P到達點B時，點Q、點P同時停止運動．設點P的運動時間為t秒，△BPQ與△ABC重疊部分面積為S．2
（1）AD=，BD=．
（2）用含t的代數式表示點Q到AB的距離．
（3）當PQ與△ABC的一邊平行時，求S的值．
（4）當點Q不與點B重合時，作點Q關于直線AB的對稱點Q'，當直線PQ′經過△ABC一邊中點時，直接寫出t的值．發布：2025/5/22 19:0:1組卷：228引用：2難度：0.1