地理老師在黑板上畫了一幅世界五大洲的圖形，并給每個洲都寫上了代號，然后，他 請5個同學每人認出2個大洲來，5個同學的回答是：
甲：3號是歐洲，2號是美洲；
乙：4號是亞洲，2號是大洋洲；
丙：1號是亞洲，5號是非洲；
丁：4號碼是非洲，3號是大洋洲；
戊：2號碼是歐洲，5號是美洲；
地理老師說：“你們每個人都認對了一半”，請問，每個號碼各代表什么洲呢？
【考點】推理與論證．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：103引用：1難度：0.5
相似題
-
1．某珠寶店失竊，甲、乙、丙、丁四人涉嫌被拘審，四人的口供如下：甲：作案的是丙；乙：丁是作案者；丙：如果我作案，那么丁是主犯；丁：作案的不是我．如果四人口供中只有一個是假的，那么以下判斷正確的是（ ）
發布：2024/12/8 14:0:3組卷：266引用：1難度：0.9 -
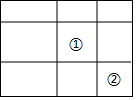2．一個大矩形按如圖方式分割成九個小矩形，且只有標號為①和②的兩個小矩形為正方形，在滿足條件的所有分割中．若知道九個小矩形中n個小矩形的周長，就一定能算出這個大矩形的面積，則n的最小值是（ ）發布：2024/12/23 18:0:1組卷：2671引用：6難度：0.7 -
3．桌子上有7張反面向上的紙牌，每次翻轉n張（n為正整數）紙牌，多次操作后能使所有紙牌正面向上嗎？用“+1”、“-1”分別表示一張紙牌“正面向上”、“反面向上”，將所有牌的對應值相加得到總和，我們的目標是將總和從-7變化為+7．
（1）當n=1時，每翻轉1張紙牌，總和的變化量是2或-2，則最少次操作后所有紙牌全部正面向上；
（2）當n=2時，每翻轉2張紙牌，總和的變化量是，多次操作后能使所有紙牌全部正面向上嗎？若能，最少需要幾次操作？若不能，簡要說明理由；
（3）若要使多次操作后所有紙牌全部正面向上，寫出n的所有可能的值．發布：2024/9/29 10:0:1組卷：877引用：10難度：0.5