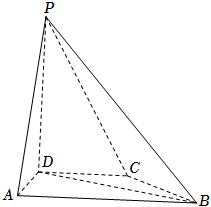
在四棱錐P-ABCD中，PD⊥底面ABCD，CD∥AB，AD=DC=CB=1，AB=2，DP=3．
（1）證明：BD⊥PA；
（2）求PD與平面PAB所成的角的正弦值．
3
【答案】（1）證明過程見解答；（2）．
5
5
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/14 5:0:1組卷：8329引用：27難度：0.6
相似題
-
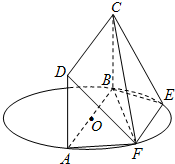1．如圖，AB為圓O的直徑，點(diǎn)E，F(xiàn)在圓上，AB∥EF，矩形ABCD所在平面與圓O所在平面互相垂直，已知AB=2，EF=1．
（Ⅰ）求證：BF⊥平面ADF；
（Ⅱ）求BF與平面ABCD所成的角；
（Ⅲ）在DB上是否存在一點(diǎn)M，使ME∥平面ADF？若不存在，請(qǐng)說明理由；若存在，請(qǐng)找出這一點(diǎn)，并證明之．發(fā)布：2025/1/20 8:0:1組卷：23引用：3難度：0.3 -
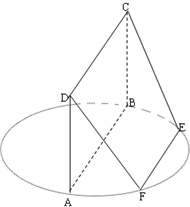2．AB為圓O的直徑，點(diǎn)E，F(xiàn)在圓上，AB∥EF，矩形ABCD所
在平面與圓O所在平面互相垂直，
已知AB=2，EF=1．
（1）求證：BF⊥平面DAF；
（2）求BF與平面ABCD所成的角；
（3）若AC與BD相交于點(diǎn)M，
求證：ME∥平面DAF．發(fā)布：2025/1/20 8:0:1組卷：29引用：3難度：0.1 -
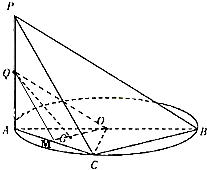3．如圖，AB是圓O的直徑，PA垂直圓O所在的平面，C是圓O上的點(diǎn)．
（1）求證：BC⊥平面PAC；
（2）設(shè)Q為PA的中點(diǎn)，G△AOC的重心，求證：QG∥平面PBC．
（3）若AC=BC=，PC與平面ACB所成的角為3，求三棱錐P-ACB的π3
體積．發(fā)布：2025/1/20 8:0:1組卷：73引用：1難度：0.7
相關(guān)試卷