2020年1月15日教育部制定出臺了《關于在部分高校開展基礎學科招生改革試點工作的意見》(也稱“強基計劃”),《意見》宣布:2020年起不再組織開展高校自主招生工作,改為實行強基計劃,強基計劃主要選拔培養有志于服務國家重大戰略需求且綜合素質優秀或基礎學科拔尖的學生,據悉強基計劃的校考由試點高校自主命題,校考過程中通過筆試后才能進入面試環節.
(1)為了更好的服務于高三學生,某研究機構對隨機抽取的5名高三學生的記憶力x和判斷力y進行統計分析,得到如表數據.
| x | 6 | 8 | 9 | 10 | 12 |
| y | 2 | 3 | 4 | 5 | 6 |
?
y
?
a
?
b
(2)現有甲、乙兩所大學的筆試環節都設有三門考試科目且每門科目是否通過相互獨立,若某考生報考甲大學,每門筆試科目通過的概率均為
2
5
1
4
,
2
3
參考公式:
①線性相關系數r=
n
∑
i
=
1
x
i
y
i
-
n
x
?
y
(
n
∑
i
=
1
x
i
2
-
n
x
2
)
(
n
∑
i
=
1
y
i
2
-
n
y
2
)
②對于一組數據(x1,y1),(x2,y2),…,(xn,yn),其回歸直線方程
?
y
=
?
b
x
+
?
a
?
b
n
∑
i
=
1
x
i
y
i
-
n
x
?
y
n
∑
i
=
1
x
i
2
-
n
x
2
?
a
y
?
b
x
【考點】經驗回歸方程與經驗回歸直線.
【答案】(1)y與x之間的關系可用線性回歸模型進行擬合,線性回歸方程為=-2.3+0.7x.
(2)m的取值范圍是(,1).
?
y
(2)m的取值范圍是(
17
60
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:401引用:5難度:0.5
相似題
-
 1.某科研機構為了了解氣溫對蘑菇產量的影響,隨機抽取了某蘑菇種植大棚12月份中5天的日產量y(單位:kg)與該地當日的平均氣溫x(單位:℃)的數據,得到如圖散點圖:
1.某科研機構為了了解氣溫對蘑菇產量的影響,隨機抽取了某蘑菇種植大棚12月份中5天的日產量y(單位:kg)與該地當日的平均氣溫x(單位:℃)的數據,得到如圖散點圖:
其中A(3,2),B(5,10),C(8,11),D(9,13),E(10,14).
(1)求出y關于x的線性回歸方程;
(2)若該地12月份某天的平均氣溫為6℃,用(1)中所求的回歸方程預測該蘑菇種植大棚當日的產量.
附:線性回歸直線方程中,?y=?bx+?a,?b=n∑i=1xiyi-nxyn∑i=1x2i-nx2.?a=y-?bx發布:2024/12/29 11:30:2組卷:104引用:3難度:0.7 -
2.某農科所對冬季晝夜溫差(最高溫度與最低溫度的差)大小與某反季節大豆新品種一天內發芽數之間的關系進行了分析研究,他們分別記錄了12月1日至12月6日每天晝夜最高、最低的溫度(如圖1),以及實驗室每天每100顆種子中的發芽數情況(如圖2),得到如下資料:
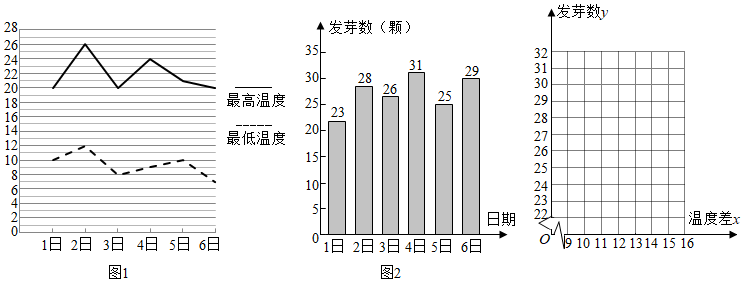
(1)請畫出發芽數y與溫差x的散點圖;
(2)若建立發芽數y與溫差x之間的線性回歸模型,請用相關系數說明建立模型的合理性;
(3)①求出發芽數y與溫差x之間的回歸方程(系數精確到0.01);?y=?a+?bx
②若12月7日的晝夜溫差為8℃,通過建立的y關于x的回歸方程,估計該實驗室12月7日當天100顆種子的發芽數.
參考數據:=2051,6∑i=1xi=75,6∑i=1yi=162,6∑i=1xiyi≈4.2,6∑i=1xi2-6x2≈6.5.6∑i=1yi2-6y2
參考公式:
相關系數:r=(當|r|>0.75時,具有較強的相關關系).n∑i=1xiyi-nx?y(n∑i=1xi2-nx2)(n∑i=1yi2-ny2)
回歸方程中斜率和截距計算公式:?y=?a+?bx=?b,n∑i=1xiyi-nx?yn∑i=1xi2-nx2=?ay-?b.x發布:2024/12/29 12:0:2組卷:189引用:5難度:0.5 -
3.兩個線性相關變量x與y的統計數據如表:
其回歸直線方程是x 9 9.5 10 10.5 11 y 11 10 8 6 5 =?yx+40,則相應于點(9,11)的殘差為 .?b發布:2024/12/29 12:0:2組卷:116引用:8難度:0.7


